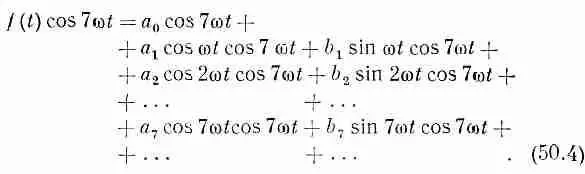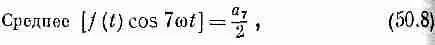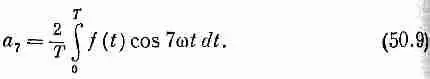Итак, мы установили правила благозвучия через совпадение гармоник. Может быть, это совпадение и является причиной благозвучия? Кто-то утверждал, что два абсолютно чистых тона, т. е. тщательно очищенных от высших гармоник, не дают ощущения благозвучия или неблагозвучия (диссонанса), когда их частоты равны или приблизительно равны ожидаемому отношению. (Это очень сложный эксперимент, поскольку приготовить чистые тоны очень трудно по причинам, которые мы увидим дальше.) Мы не можем с уверенностью сказать, сравнивает ли ухо гармоники или занимается арифметикой, когда мы решаем, что звук нам нравится.
§ 4. Коэффициенты Фурье
Вернемся теперь к утверждению о том, что каждую ноту, т. е. любое периодическое колебание, можно представить в виде надлежащей комбинации гармоник. Хотелось бы знать, как можно найти нужную долю каждой гармоники. Конечно, если нам даны все коэффициенты а и b , то, пользуясь формулой (50.2), легко подсчитать функцию f(t). Теперь же вопрос состоит в том, как можно найти коэффициенты при различных гармониках, если нам задана функция f(t)? (Нетрудно испечь пирог, если есть рецепт, но как, отведав пирог, написать его рецепт?)
Фурье открыл, что на самом деле сделать это не очень трудно. Член а 0 уж наверняка нетрудно найти. Мы говорили, что он равен среднему значению f ( f ) на протяжении одного периода (от t=0 до t = T ). Легко увидеть, что это действительно так. Среднее значение синуса или косинуса на протяжении одного периода равно нулю. На протяжении двух, или трех, или другого целого числа периодов оно тоже равно нулю. Таким образом, среднее значение всех членов с правой стороны (50.2), за исключением только а 0, равно нулю. (Напомним, что мы должны выбрать w=2p/T.)

Далее, поскольку среднее значение суммы равно сумме средних, то среднее значение функции f ( t ) равно просто среднему от а 0. Но ведь а 0— просто постоянная, и ее среднее значение равно ей самой. Вспоминая определение среднего, мы получаем
Найти остальные коэффициенты ненамного труднее. Чтобы сделать это, используем один фокус, открытый самим Фурье. Предположим, что мы умножили обе стороны уравнения (50.2) на какую-то гармоническую функцию, скажем на cos 7 w t . При этом получается
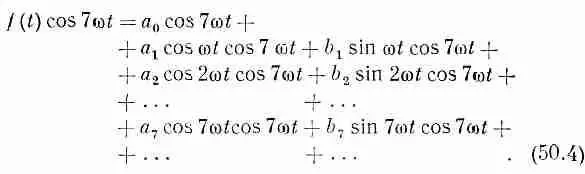
А теперь усредним обе стороны равенства. Среднее от члена a 0cos7wt по периоду Т пропорционально среднему от косинуса по семи его периодам. Но последнее просто равно нулю. Среднее почти всех остальных членов тоже будет равно нулю. Действительно, давайте рассмотрим член с а 1 . Мы знаем, что в общем случае
cos A cos В = 1/ 2cos (А +B)+ 1/ 2cos (А - В), (50.5)
так что член с а 1 равен
a 1(cos8wt+cos6wt). (50.6)
Таким образом получаются два косинуса: один с восемью полными периодами, а другой с шестью. Оба они равны нулю. Поэтому среднее значение этого члена тоже равно нулю.
Для члена с а 2мы получаем cos9wt и cos5wt, каждый из которых при усреднении превратится в нуль. Для члена с а 9 получится соз16wt и cos(- 2 w t ). Но cos(-2wt) — это то же самое, что cos2wt, так что опять оба члена дадут при усреднении нуль. Ясно, что все слагаемые с косинусами, за исключением одного, дадут при усреднении нуль. Этим единственным слагаемым будет член с а 7 . Для него же мы получим
1/ 2a 7(cos14wt+cos0). (50.7)
Косинус нуля равен единице, а среднее от него, разумеется, тоже равно единице. Итак, мы получили, что среднее от всех членов с косинусами уравнения (50.4) равно 1/ 2а 7 .
Еще легче расправиться с синусами. Когда мы умножаем их накосинус типа cos n w t , то таким же методом можно показать, что все они при усреднении обращаются в нуль.
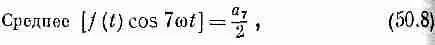
Мы видим, что способ, придуманный Фурье, действует как своеобразное сито. Когда мы умножаем на cos7wt и усредняем, то все члены, кроме а 7, отсеиваются и в результате остается
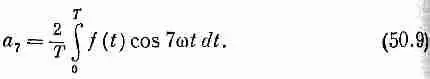
Читать дальше