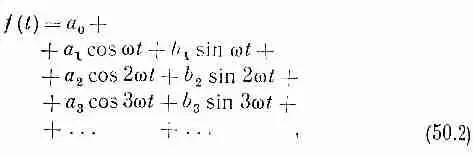Feynmann - Feynmann 4a

До сих пор мы говорили о движении струны. Однако звук, который представляет собой движение воздуха, вызванное дви­жением струны, тоже должен состоять из тех же гармоник, хотя здесь мы уже не можем говорить о собственных гармониках воздуха. К тому же относительная сила различных гармоник в воздухе может быть совсем другой, чем в струне, особенно если струна «связана» с воздухом посредством «звучащей дос­ки». Разные гармоники по-разному связаны с воздухом.

Если для музыкального тона функция f ( t ) представляет давление воздуха в зависимости от времени (скажем, такая, как на фиг. 50.1.б), то можно ожидать, что f ( t ) записывается в виде суммы некоторого числа простых гармонических функ­ций от времени (подобных cosw t ) для каждой из различных гармонических частот. Если период колебаний равен Т, то основная угловая частота будет w =2 p /Т, а следующие гармо­ники будут 2w, Зw и т. д.

Здесь появляется небольшое усложнение. Мы не вправе ожидать, что для каждой частоты начальные фазы обязательно будут равны друг другу. Поэтому нужно пользоваться функ­циями типа cos(wt+j). Вместо этого, однако, проще исполь­зовать для каждой частоты как синус, так и косинус. Напом­ним, что

cos w t + j)=cosjcosw t - sinjsinw t , (50.1)

а поскольку j — постоянная, то любые синусоидальные коле­бания с частотой w могут быть записаны в виде суммы членов, в один из которых входит sinwt, а в другой — cos w t .

Итак, мы приходим к заключению, что любая периодиче­ская функция f ( t ) с периодом Т математически может быть за­писана в виде

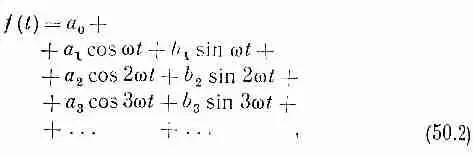
где w=2p/T, a a и b — числовые постоянные, указывающие, с каким весом каждая компонента колебания входит в общее колебание f ( t ). Для большей общности мы добавили в нашу формулу член с нулевой частотой а 0 , хотя обычно для музы­кальных тонов он равен нулю. Это просто сдвиг средней вели­чины звукового давления (т. е. сдвиг «нулевого» уровня). С этим членом наша формула верна для любого случая. Уравне­ние (50.2) схематически показано на фиг. 50.2.

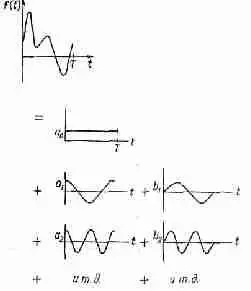
Фиг. 50.2. Любая периодическая функция f ( t ) равна сумме про­стых гармонических функций.

Амплитуды гармонических функций а n и b n выбираются по специально­му правилу. На рисунке они показаны только схематически без соблюдения масштаба. [Ряд (50.2) называется рядом Фурье для функций f(t).]

Мы сказали, что любую периодическую функцию можно написать в таком виде. Следует внести небольшую поправку и подчеркнуть, что в такой ряд можно разложить вообще любую звуковую волну или любую функцию, с которой мы сталки­ваемся в физике. Математики, конечно, могут придумать такую функцию, что ее нельзя будет составить из простых гармо­нических (например, функцию, которая «заворачивает» назад, так что для некоторых величин t она имеет два значения!). Однако здесь нам не стоит беспокоиться о таких функциях.

§ 3. Качество и гармония

Теперь мы уже можем описать, чем определяется «качество» музыкального тона. Оно определяется относительным количе­ством различных гармоник, т. е. относительными величинами а и b . Тон, содержащий только первую гармонику, называется «чистым», а тон с несколькими сильными гармониками назы­вается «богатым». Скрипка дает гармоники в одной пропорции, а гобой — в другой.

Можно «изготовить» различные музыкальные тоны, если подсоединить к громкоговорителю несколько «осцилляторов». (Осциллятор обычно дает приблизительно чистые простые гар­монические колебания) В качестве частот осцилляторов мы выберем w, 2w, Зw и т. д. Приделав к каждому осциллятору ре­гулятор громкости, можно смешивать гармоники в любой же­лаемой пропорции и тем самым создавать звуки различного качества. Примерно так работает электрический орган. Кла­виши выбирают частоту основного осциллятора, а педали кон­тролируют относительную пропорцию различных гармоник. С помощью этих регуляторов можно заставить орган звучать как флейту, или как гобой, или как скрипку.

Интересно, что для получения такого «искусственного» звука нет никакой необходимости разделять осцилляторы на «синусные» и «косинусные» — для каждой частоты нам достаточно только одного осциллятора. Наше ухо не очень чувствительно к относительной фазе гармоник. Оно воспринимает «синусную» и «косинусную» части частоты в целом. Поэтому наш анализ более точен, чем это необходимо для объяснения субъективной стороны музыки. Однако реакция микрофона или другого физического инструмента все-таки зависит от фазы, и наш пол­ный анализ для таких случаев просто необходим.