Feynmann - Feynmann 4a

На фиг. 49.2 показаны первые три собственные гармоники нашей струны.

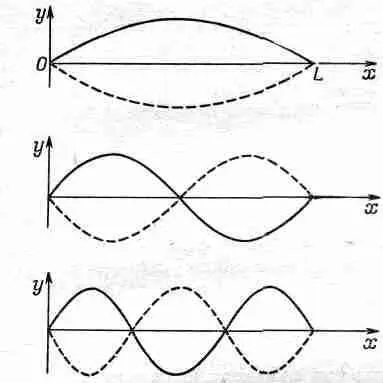
Фиг. 49.2. Первые три гар­моники колеблющейся струны.

Длина волны l первой из них равна 2L. В этом легко убедиться, продолжив волну до точки x =2 L и получив полный цикл синусоидальной волны. Угловая частота w равна в общем случае 2pc, деленному на длину волны К, а поскольку сейчас у нас l= 2 L , то частота будет равна p с/ b , что согласуется с формулой (49.6) при n=1. Обозначим эту частоту через w 1Следующая собственная гармоника напоми­нает бантик из двух петель с узлом посредине. Ее длина просто равна L . Соответствующая величина k , а следовательно, и ча­стота w должны быть вдвое большими, т. е частота равна 2w 1. Частота третьей собственной гармоники оказывается рав­ной Зw 1и т. д. Таким образом, различные собственные гармо­ники кратны целому числу низшей частоты w 1т. е. w 1, 2 w 1 , Зw 1и т. д.

Вернемся теперь к общему движению струны. Оказывается, что любое возможное движение можно рассматривать как одно­временное действие некоторого числа собственных колебаний. На самом деле для описания наиболее общего движения долж­но быть одновременно возбуждено бесконечное число собствен­ных гармоник. Чтобы получить некоторое представление о том, что происходит при таком сложении, давайте посмотрим, что получится при одновременном колебании двух первых соб­ственных гармоник. Пусть первая из них колеблется так, как это показано в ряде схематических чертежей фиг. 49.3, где изображены отклонения струны через равные промежутки вре­мени на протяжении полуцикла низшей частоты.

Предположим теперь, что одновременно с первой собствен­ной гармоникой работает и вторая. Последовательные положе­ния струны при возбуждении этой собственной гармоники показаны тоже на фиг. 49.3 пунктирной линией. По отношению к первой гармонике они сдвинуты по фазе на 90°. Это означает, что в начальный момент никакого отклонения не было, но ско­рости двух половинок струны направлены в противоположные стороны. Вспомним теперь общий принцип линейных систем: если взять любые два решения, то сумма их тоже будет реше­нием. Поэтому перемещения, полученные сложением двух ре­шений, показанных на фиг. 49.3, будут третьим возможным ре­шением

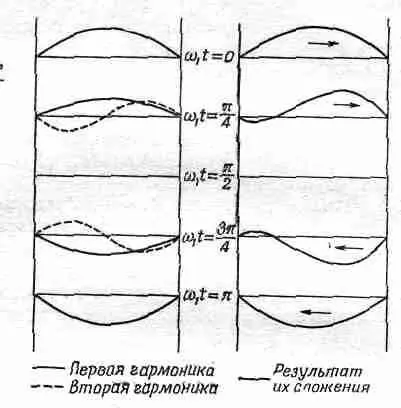
Фиг. 49. 3 . Две гармоники, напоминающие при сложе­нии бегущую волну.

На этом же рисунке показан и результат сложения, который начинает напоминать горб, пробегающий взад и вперед по струне от одного конца до другого, хотя с помощью только двух собственных гармоник нельзя построить доста­точно хорошей картины такого движения; их нужно гораздо больше. Этот результат представляет на самом деле частный случай основного принципа линейных систем, который гла­сит:

Любое движение можно рассматривать как составленное из различных собственных гармоник, взятых с надлежащими ам­плитудами и фазами.

Значение этого принципа обусловлено тем фактом, что каж­дое собственное колебание — очень простая вещь — это просто синусоидальное движение во времени. По правде говоря, даже общее движение струны — еще не самая сложная вещь; суще­ствует движение куда более сложное, скажем такое, как виб­рация крыльев самолета. Тем не менее даже у крыльев само­лета можно обнаружить некие собственные кручения с опре­деленными частотами. А если так, то полное движение можно рассматривать как суперпозицию гармонических колебаний (за исключением тех случаев, когда вибрация настолько велика, что система уже не может рассматриваться как линейная).

§ 3. Двумерные собственные колебания

Сейчас мы перейдем к рассмотрению очень интересного поведения собственных гармоник в двумерных колебаниях. До сих пор мы говорили только об одномерных колебаниях: натянутой струне или звуковых волнах в трубе. В конце концов мы должны добраться до трех измерений, но сначала давайте остановимся на более легком этапе — этапе двумерных колеба­ний. Возьмем для большей определенности прямоугольный ре­зиновый барабан, перепонка которого закреплена по краям так, что на прямоугольном крае барабана она перемещаться не может. Пусть размеры прямоугольника будут