Feynmann - Feynmann 4a

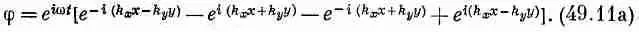
равны а и 6, как это показано на фиг. 49.4.

Фиг. 49.4. Колебание прямо­угольной пластинки.

Прежде всего, каковы ха­рактеристики возможного движения? Можно начать с того же, с чего мы начали, когда рассматривали пример со стру­ной. Если бы никакого закрепления не было вовсе, то можно было бы ожидать появления волн, бегущих в некото­ром направлении, например синусоидальной волны, опи­сываемой функцией ехр(iwt) ехр[- i ( k ч x )+ i ( k y y )], направле­ние движения которой зависит от относительной величины чисел k x и k y . А как теперь сделать узел на оси х, т. е. при y=0? Используя ту же идею, что и для одномерной струны, можно добавить волну, описываемую комплексной функцией

-exp(iwt)ехр[- i(k x x)-i(k y y)].

Суперпозиция этих волн в результате дает нулевое переме­щение при y=0 независимо от того, каковы будут значения х и t . (Хотя эти функции будут определены и для отрицательных значений у там, где никакого барабана нет и колебаться не­чему, но на это можно не обращать никакого внимания. Ведь нам хотелось устранить перемещение при у=0, и мы добились этого.) Вторую функцию в этом случае можно рассматривать как отраженную волну.

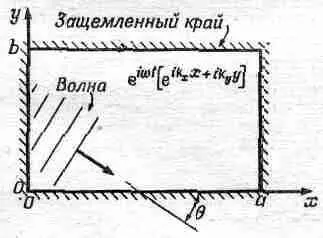
Однако нам нужно получить узел не только на линии y=0, но и на линии у = b . Как же это сделать? Решение такой задачи связано с некоторыми вещами, которыми мы занимались при изучении отражения света от кристалла. Волны, гасящие друг друга при y=0, могут сделать то же самое и при у = b , только когда 2 b sin 0 равно целому числу длин волн l, (q — угол, пока­занный на фиг. 49.4):

ml=2bsinq, m=0, 1, 2, .... (49.7)

Точно таким же образом, т.е. сложением еще двух функций [-exp ( i w t )] exp [ i ( k x x )+ i ( k y y )] и [+ exp ( i c t )} exp [ i ( k x x )- i ( k y y )], каждая из которых представляет отражение другой от линии х=0, можно устроить узел и на оси у. Условие того, что линия х=а будет тоже узловой, получается так же, как и условие при у= b , т. е. 2acosq должно быть равно целому числу длин волн:

nl = 2acosq. (49.8)

Тогда окончательный результат таков: волны, «заключенные» в ящике, имеют вид стоячей волны, т. е. образуют какие-то определенные собственные гармоники.

Таким образом, если мы хотим иметь дело с собственными гармониками, то должны удовлетворить двум написанным выше условиям. Для начала давайте найдем длину волны. Ис­ключив из уравнений (49.7) и (49.8) угол q, можно выразить длину волны через a, b , n и т. Легче всего это сделать так: сначала разделить обе части уравнений соответственно на 2 b и 2a, а затем возвести их в квадрат и сложить. В результате мы получим уравнение

sin 2q+cos 2q =1=(nl/2a) 2+(ml/2b) 2,

которое легко разрешить относительно l:

Итак, мы определили длину волны через два целых числа, а по длине волны мы немедленно получаем частоту w, ибо, как известно, частота равна 2pc, деленной на длину волны.

Этот результат настолько важен и интересен, что необхо­димо теперь получить его строго математически без использо­вания аналогий с отражением. Давайте представим колебание в виде суперпозиции четырех волн, подобранных таким обра­зом, чтобы все четыре линии x=0, х = а, y =0 и у= b были узло­выми. Потребуем еще, чтобы все эти волны имели одинаковую частоту, т. е. чтобы результирующее движение представляло собственное колебание. Из главы об отражении света мы уже знаем, что функция exp(iwt)exp[- i ( k x x )+ i ( k y y )] опи­сывает волну, идущую в направлении, указанном на фиг. 49.4. По-прежнему остается справедливым уравнение (49.6), т. е. k =w/c, с той разницей, что теперь

k 2=k 2 x+k 2 y. (49.10)

Из рисунка ясно, что k x = kcos q , a k y = k sinq.

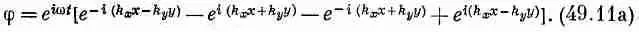
Таким образом, наше выражение для перемещения прямо­угольной перепонки барабана (назовем это перемещение j запишется в виде