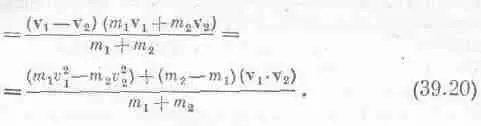Feynmann - Feynmann 4

< w· v ц.м.>=0. (39.19)

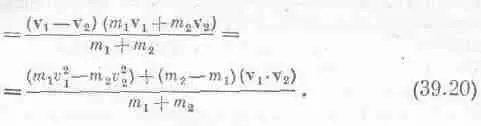
Скалярное произведение w·v ц.м.легко выразить через v 1и v 2:

Займемся сначала v 1·v 2; чему равно среднее v 1·v 2? Иначе го­воря, чему равно среднее проекции скорости одной молекулы на направление скорости другой молекулы? Ясно, что вероят­ности движения молекулы как в одну сторону, так и в проти­воположную одинаковы. Среднее значение скорости v 2 в любом направлении равно нулю. Поэтому и в направлении v 1среднее значение v 2тоже равно нулю. Итак, среднее значение v 1·v 2равно нулю! Следовательно, мы пришли к выводу, что среднее т 1 v 2 1 должно быть равно т 2 v 2 2 . Это значит, что средние кинети­ческие энергии обеих молекул должны быть равны :

1/ 2m 1v 2 1= 1/ 2m 2v 2 2. (39.21)

Если газ состоит из атомов двух сортов, то можно показать (и мы даже считаем, что нам удалось это сделать), что средние кинетические энергии атомов каждого сорта равны, когда газ находится в состоянии равновесия. Это означает, что тяжелые атомы движутся медленнее, чем легкие; это легко проверить, поставив эксперимент с «атомами» различных масс в воздушном желобе.

Теперь сделаем следующий шаг и покажем, что если в ящи­ке имеются два газа, разделенные перегородкой, то по мере достижения равновесия средние кинетические энергии атомов разных газов будут одинаковы, хотя атомы и заключены в разные ящики. Рассуждение можно построить по-разному. Например, можно представить, что в перегородке проделана маленькая дырочка (фиг. 39.4), так что молекулы одного газа проходят сквозь нее, а молекулы второго слишком велики и не пролезают.

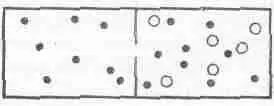
Фиг. 39. 4. Два газа в ящике, разделенном полупроницаемой пере­городкой.

Когда установится равновесие, то в том отделе­нии, где находится смесь газов, средние кинетические энергии молекул каждого сорта сравняются. Но ведь в числе проник­ших сквозь дырочку молекул есть и такие, которые не потеря­ли при этом энергии, поэтому средняя кинетическая энергия молекул чистого газа должна быть равна средней кинетичес­кой энергии молекул смеси. Это не очень удовлетворительное доказательство, потому что ведь могло и не быть такой дырочки, сквозь которую пройдут молекулы одного газа и не смогут прой­ти молекулы другого.

Давайте вернемся к задаче о поршне. Можно показать, что кинетическая энергия поршня тоже должна быть равна 1/ 2 m 2 v 2 2 . Фактически кинетическая энергия поршня связана только с его горизонтальным движением. Пренебрегая возмож­ным движением поршня вверх и вниз, мы найдем, что гори­зонтальному движению соответствует кинетическая энергия 1/ 2m 2v 2 2 x. Но точно так же, исходя из равновесия на другой сто­роне, можно показать, что кинетическая энергия поршня долж­на быть равна 1/ 2 т 1 v 2 1 x . Хотя мы повторяем предыдущее рас­суждение, возникают некоторые дополнительные трудности в связи с тем, что в результате столкновений средние кинети­ческие энергии поршня и молекулы газа сравниваются, потому что поршень находится не внутри газа, а смещен в одну сто­рону.

Если вас не удовлетворит и это доказательство, то можно придумать искусственный пример, когда равновесие обеспечи­вается устройством, по которому молекулы каждого газа бьют с обеих сторон. Предположим, что сквозь поршень проходит короткий стержень, на концах которого насажено по шару. Стержень может двигаться сквозь поршень без трения. По каж­дому из шаров со всех сторон бьют молекулы одного сорта. Пусть масса нашего устройства равна m , а массы молекул газа, как и раньше, равны m 1 и m 2. В результате столкновений с молекулами первого сорта кинетическая энергия тела массы m равна среднему значению 1/ 2 m t v 2 1 (мы уже доказали это). Точно так же, столкновения с молекулами второго сорта зас­тавляют тело иметь кинетическую энергию, равную среднему значению 1 / 2 m z v 2 2 . Если газы находятся в тепловом равнове­сии, то кинетические энергии обоих шаров должны быть рав­ны. Таким образом, результат, доказанный для случая смеси газов, можно немедленно обобщить на случай двух разных газов при одинаковой температуре.