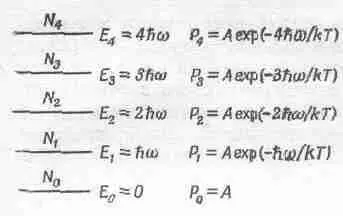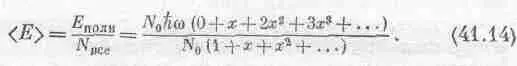Feynmann - Feynmann 4

За изучение этой кривой взялся Планк. Сначала он нашел чисто эмпирический ответ, сравнивая опытную кривую с из­вестными функциями, которые лучше всего эту кривую подгоняли. Таким образом, он получил эмпирическую формулу для средней энергии гармонического осциллятора как функцию температуры. Иначе говоря, он заменил kT правильной фор­мулой, а потом нашел простой вывод этой формулы, правда, при очень странном предположении. Это предположение со­стоит в том, что гармонический осциллятор может поглотить за один прием только энергию h w. После этого нельзя и подумать, что осциллятор может обладать любой энергией. Конечно, это было началом конца классической физики.

Сейчас мы выведем первую правильную формулу квантовой механики. Предположим, что дозволенные уровни энергии гармонического осциллятора лежат на равном расстоянии hw 0друг от друга, поэтому осциллятор может обладать только одной из этих энергий (фиг. 41.5).

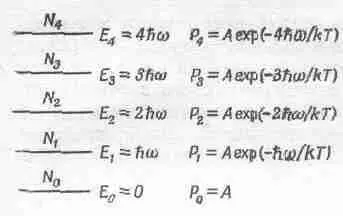
Фиг. 41.5, Уровни энергии гар­монического осциллятора.

Отстоят друг от друга но равных рас­стояниям E n = nh w .

Аргументы Планка выглядят немного сложнее наших, ведь это было самым началом кванто­вой механики, и ему приходилось кое-что доказывать. Ну, а мы просто примем как факт (который Планк и установил), что вероятность того, что занят уровень энергии Е, равна Р(Е)= a ехр( - E / kT ). Исходя из этого, мы получим правильный результат.

Предположим, что у нас есть много осцилляторов и каждый колеблется с частотой w 0. Некоторые из них находятся в низ­шем квантовом состоянии, другие забрались на уровень выше и т. д. Нам нужно знать среднюю энергию этих осцилля­торов. Чтобы найти ее, давайте вычислим полную энергию всех осцилляторов и поделим результат на их число. Тогда мы получим среднюю энергию на осциллятор при тепловом равновесии, а это то же самое, что и энергия при равновесии с излучением черного тела, и ее надо подставить в уравнение. (41.13) вместо kT .

Пусть N 0 — число осцилляторов в основном состоянии (состоянии с наименьшей энергией), N 1 — число осцилляторов в состоянии Е 1 , n 2 — число осцилляторов в состоянии E 2 и т. д. Согласно гипотезе (которую мы не доказали), классические выражения для вероятности ехр(-п. э./kT) или ехр(-к. э. / kT ) заменяются в квантовой механике на ехр(-D E / kT ), где DE — разность энергий, Можно утверждать, что число осцилляторов в первом состоянии N 1 равно произведению числа молекул в основном состоянии N 0 на ехр(-hw/kT). Аналогично, n 2 (число молекул во втором состоянии) равно N 2 = N 0 exp(-2hw/kT). Чтобы упростить алгебру, введем х= ехр(-hw / kT ). Тогда все выглядит очень просто:

N 1 =N 0 x, N 2= N 0 x 2 ..., N n =N 0 x n .

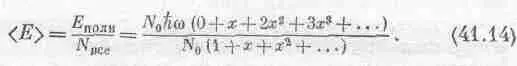
Сначала найдем полную энергию всех осцилляторов. Если осциллятор находится в основном состоянии, его энергия нуль. Если он находится в первом состоянии, то его энергия равна hw 0, а таких осцилляторов N 1 . З начит, в этом состоянии запасена энергия N 1 h w , или h w N 0 x . Энергия осцил­лятора во втором состоянии 2hw 0, а осцилляторов N 2 , поэтому мы получаем такую энергию: N22hw=2hw 0N 0x 2и т. д. Сложив все это, найдем полную энергию E полн = N 0 h w ( 0+ х + 2х 2 + З x 3 +...). А сколько всего осцилляторов? В основном состоянии, ко­нечно, N 0 , в первом состоянии N l и т. д.; снова все сложим и получим N в c е = N 0 (1+ x + x 2 + x 3 +...). Поэтому средняя энергия равна

Читателям представляется возможность позабавиться этими суммами и получить от этого удовольствие. Когда вы покон­чите с суммированием и подставите в окончательный результат значение х, то получите, если не ошиблись