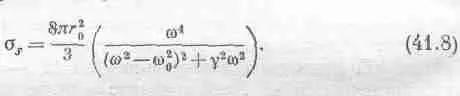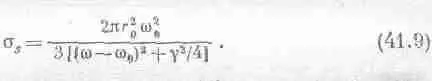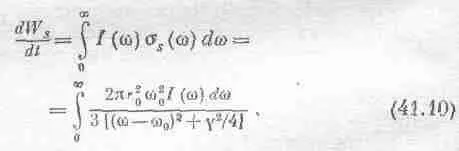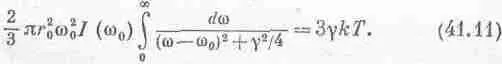Feynmann - Feynmann 4

Сколько же все-таки света поглотится? Мы уже определяли количество излучения, поглощаемого из заданного падающего пучка света, и выразили его через эффективное сечение. Это соответствует тому, как если бы мы предполагали, что весь свет, падающий на площадку определенной площади, погло­щается. Таким образом, полная переизлученная (рассеянная) интенсивность равна произведению интенсивности падающего света I(w)dw на эффективное сечение а.

Мы вывели формулу для эффективного сечения [см. уравне­ние (31.19)1, не включающую затухания. Нетрудно повторить этот вывод снова и учесть трение, которым мы тогда пренебре­гли. Если это сделать, то, вычисляя эффективное сечение по прежнему образцу, мы получим

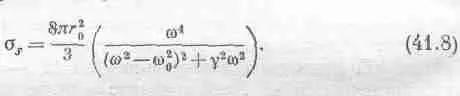
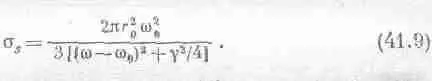
Пойдем дальше; s s как функция частоты имеет более или менее заметную величину только для w около собственной час­тоты w 0. (Вспомним, что для излучающего осциллятора Q — порядка 10 8.) Когда со равна w 0, осциллятор рассеивает очень сильно, а при других значениях w он почти не рассеивает сов­сем. Поэтому можно заменить w на w 0, а w 2-w 2 0на 2w 0(w-w 0); тогда

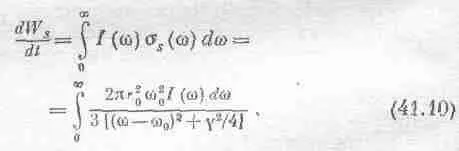
Теперь почти вся кривая загнана в область около w=w 0. (Фактически мы не должны делать никаких приближений, но легче иметь дело с интегралом, в котором подынтегральное вы­ражение несколько проще.) Если умножить интенсивность в данном интервале частот на эффективное сечение рассеяния, то получится энергия, рассеянная в интервале dw. Полная рассеянная энергия — это интеграл по всем w. Таким образом,

Теперь мы положим dW s / dt =3 g kT . Но почему здесь стоит 3? Потому что в гл. 32 мы предполагали, что свет поляризован так, что может раскачивать осциллятор. Если бы мы исполь­зовали осциллятор, способный раскачиваться только в одном направлении, а свет был бы, скажем, поляризован неверно, то он не рассеивался бы совсем. Поэтому мы должны либо усреднить эффективное сечение рассеяния на осцилляторе, способном раскачиваться только в одном направлении, по всем направле­ниям падающих пучков и поляризации света в пучке, либо, что легче сделать, представить себе, что наш осциллятор пос­лушно следует за полем, каким бы оно ни было там, где он на­ходится. Такой осциллятор, который одинаково легко раска­чивается в любом из трех направлений, имеет среднюю энергию 3 kT , потому что у него 3 степени свободы. А раз 3 степени сво­боды, то надо писать 3 g kT .

Займемся теперь интегралом. Предположим, что неизвест­ное спектральное распределение света I(w) — это плавная кри­вая, которая в той узкой области частот, где s sимеет острый максимум, меняется не слишком сильно (фиг. 41.3).

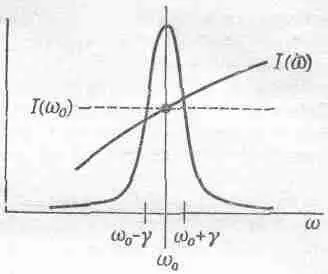
Фиг. 41.3. Сомножители подын­тегрального выражения (41.10).

Пик — это резонансная кривая 1 /[( w - w 0 ) 2 + ( g 2 / 4 )]. Множитель I ( w ) можно с хорошим приближением за­менить на I ( w 0 ).

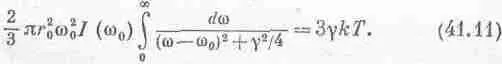
Тогда сколь­ко-нибудь существенный вклад в интеграл дают только частоты, близкие к w 0и отстоящие от нее на очень малую величину g. Поэтому, хотя I(w) неизвестная и, может быть, сложная функ­ция, важно только ее поведение около w=w 0и можно заменить плавную кривую еще более ровной — «постоянной» — всюду одной высоты. Иначе говоря, мы просто вынесем I(w) из-под знака интеграла и назовем это I(w 0). Вынесем за интеграл и остальные постоянные и тогда получим

Интеграл берется от 0 до Ґ, но 0 отстоит так далеко от w 0, что кривая за это время идет почти вдоль оси абсцисс, поэтому заменим 0 на -Ґ, разница небольшая, а интеграл взять легче.

Интеграл вида ∫ dx /( x 2 +а 2 ) приводит к арктангенсу. Если

взглянуть в справочник, то мы увидим, что он равен я/а. Итак, для нашего случая это 2p/g. После небольших манипуляций мы получаем