Те же флуктуации работают, и довольно удивительным образом, в электрических цепях. Предположим, что мы построили очень чувствительный, точный усилитель для какой-нибудь определенной частоты и к его входу подключили резонансную цепь (фиг. 41.2), настроенную на эту же частоту, наподобие радиоприемника, только получше.
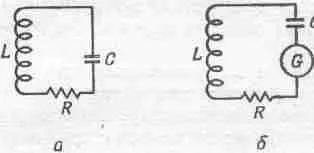
Фиг. 41,2. Резонансная цепь с большим Q .
а — реальная цепь при температуре T ; б — искусственная цепь с идеальным (бесшумным) сопротивлением и «генератором шума».
Предположим, что мы захотели как можно точнее изучить флуктуации, для этого мы сняли напряжение, скажем, с индуктивности и подали его на усилитель. Конечно, во всякой цепи такого рода имеются некоторые потери. Это не идеальная резонансная цепь, но все же очень хорошая цепь, и обладает она малым сопротивлением (на схеме сопротивление показано, надо только помнить, что оно очень мало). А теперь мы хотим узнать, как велики флуктуации падения напряжения на индуктивности? Ответ: Нам известно, что «кинетическая энергия», запасенная катушкой резонансной цепи, равна 1/ 2 LI 2 (см. гл. 25). Поэтому среднее значение 1/ 2 LI 2 равно 1/ 2 kT , это дает нам среднее квадратичное значение тока, а отсюда можно определить и среднее квадратичное значение напряжения. Если мы хотим знать падение напряжения на индуктивности, нам пригодится формула 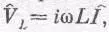 , тогда средний квадрат модуля падения напряжения на индуктивности равен 2 L> = L 2w 2 02>, a полагая 1/ 2L2> = 1/ 2 kT , получаем
, тогда средний квадрат модуля падения напряжения на индуктивности равен 2 L> = L 2w 2 02>, a полагая 1/ 2L2> = 1/ 2 kT , получаем
< V 2 L >= L w 2 0 kT . ... (41.2)
Итак, теперь мы можем рассчитать контур и предсказать, каким в нем будет так называемый шум Джонсона, т. е. шум, связанный с тепловыми флуктуациями!
Но откуда же эти флуктуации берутся? А все из-за сопротивления, точнее говоря, в результате пляски электронов в сопротивлении. Ведь они находятся в тепловом равновесии с остальным материалом сопротивления, а это приводит к флуктуациям плотности электронов. Таким образом они порождают крошечные электрические поля, управляющие резонансной цепью.
Инженеры-электрики объясняют все это иначе. Физически источником шумов служит сопротивление. Однако можно заменить реальную цепь с честным сопротивлением, вызывающим шумы, фиктивной цепью, содержащей маленький генератор, который якобы порождает шумы, а сопротивление теперь будет идеальным — оно уже не шумит. Все шумы теперь исходят от фиктивного генератора. Итак, если нам известны характеристики шума, порождаемого сопротивлением, и у нас для этого имеется подходящая формула, то можно рассчитать, как цепь реагирует на этот шум. Следовательно, нам нужна формула для шумовых флуктуации. Сопротивление одинаково хорошо порождает шумы всех частот, поскольку оно само отнюдь не резонатор. Резонансная цепь, конечно, «слышит» лишь часть этого шума вблизи определенной частоты, а в сопротивлении заключено много и других частот. Силу генератора можно описать таким образом: выделяемая на сопротивлении средняя мощность, если оно непосредственно соединено с генератором шума, равна 2>/R, где Е — снимаемое с генератора напряжение. Но теперь мы хотим знать подробнее о распределении мощности по частотам. Каждой определенной частоте соответствует очень малая мощность. Пусть P(w)dw — мощность, которую генератор посылает сопротивлению в интервале частот d w . Тогда можно доказать (мы докажем это для другого случая, но математика и там и тут одинакова), что выделяемая мощность равна
P ( w ) d w =2/ p kTd w (41.3) я, таким образом, не зависит от сопротивления.
§ 2 . Тепловое равновесие излучения
Мы приступаем к обсуждению более сложной и интересной теоремы, суть которой состоит в следующем. Предположим, что у нас имеется заряженный осциллятор, вроде того, о котором мы говорили, когда речь шла о свете. Пусть это будет электрон, колеблющийся в атоме вверх и вниз. А раз он колеблется, то излучает свет. Предположим теперь, что этот осциллятор попал в сильно разреженный газ, состоящий из других атомов, и время от времени эти атомы с ним сталкиваются. Когда в конце концов наступит равновесие, осциллятор приобретает такую энергию, что кинетическая энергия колебаний будет равна l / 2 kT , а поскольку это гармонический осциллятор, то полная энергия движения станет равной kT .
Читать дальше

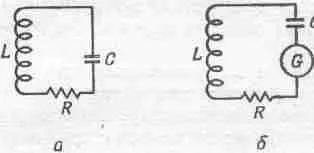
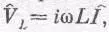 , тогда средний квадрат модуля падения напряжения на индуктивности равен 2 L> = L 2w 2 02>, a полагая 1/ 2L2> = 1/ 2 kT , получаем
, тогда средний квадрат модуля падения напряжения на индуктивности равен 2 L> = L 2w 2 02>, a полагая 1/ 2L2> = 1/ 2 kT , получаем










