Feynmann - Feynmann 4

Читатель легко может проверить, что число столкновений, которые испытывает одна плавающая в воде молекула, порядка 10 14в секунду, так что на одну сотую долю секунды приходится примерно 10 12столкновений, а это очень много! Естественно, что по прошествии одной сотой доли секунды частица не «по­мнит», что с ней было до этого. Иначе говоря, все столкновения случайны, так что каждый последующий «шаг» частицы совер­шенно не зависит от предыдущего. Это напоминает знаменитую задачу о пьяном моряке, который выходит из бара и делает несколько шагов, но плохо держится на ногах, и каждый шаг делает куда-то в сторону, случайно (фиг. 41.6).

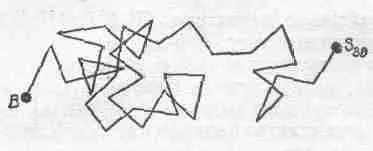
Фиг. 41.6. Зигзагооб­разный путь из 36 слу­чайных шагов длиной L .

Как далеко расположена точка S 36 от В? В среднем на 6 L .

Так где же окажется наш матрос спустя некоторое время? Конечно, мы этого не знаем! И предсказать это невозможно. Все, что можно сказать, — это то, что он где-то наверняка находится, но это совершенно неопределенно. Ну хорошо, а далеко ли он все-таки уйдет? Каково будет то среднее расстояние от бара, на котором окажется матрос? На этот вопрос мы уже ответили, потому что мы однажды уже обсуждали суперпозицию света от огромного числа различных источников с различными фазами, а это значит, что мы складывали огром­ное число стрелок, направленных по произвольным направ­лениям (см. гл. 32) Тогда мы обнаружили, что средний квадрат расстояния от одного конца цепи беспорядочных шагов до другого (т. е. интенсивность света) равен сумме интенсивностей отдельных источников. Совершенно аналогично, используя ту же математику, можно немедленно показать, что если R N— векторное расстояние от начала через N шагов, то средний квадрат расстояния от начала пропорционален числу шагов N.

Это значит, что < R 2 N >= NL 2 , где L — длина каждого шага. Поскольку число шагов пропорционально выделенному нам условиями задачи времени, то средний квадрат расстояния пропорционален времени:

2>=at. (41.17)

Это не означает, что среднее расстояние пропорционально времени. Если бы среднее расстояние было пропорционально времени, то частица двигалась бы с вполне определенной по­стоянной скоростью. Матрос, несомненно, идет вперед, но движение его таково, что квадрат среднего расстояния про­порционален времени. Это и есть характерная особенность случайных блужданий.

Мы легко докажем, что каждый шаг увеличивает квадрат расстояния в среднем на L 2. Если записать R N= R N -1+ L, то окажется, что R 2 Nравно

R N· R N=R 2 N= R 2 N - I + 2 R N -1· L+ L 2 ,

а усредняя по многим попыткам, получим 2 N>=2 N -1>+L 2, потому что < R N -1· L>=0. Таким образом, по индукции

R 2 N = NL 2 (41.18)

Теперь хорошо бы вычислить коэффициент a в уравнении (41.17); для этого нужно еще кое-что добавить. Предположим, что если к частице приложена сила (она не имеет никакого отношения к броуновскому движению, просто мы подыскиваем выражение для импульса), то частица будет противодействовать силе следующим образом. Прежде всего должна проявиться инерция. Пусть m — коэффициент инерции, эффективная масса частицы (не обязательно настоящая масса настоящей частицы, потому что если протаскивать частицу сквозь воду, то дви­жется и вода). Поэтому если мы рассматриваем движение в одном направлении, то нужно обзавестись с одной стороны слагаемым m ( d 2 x / dt 2 ). Далее подчеркнем, что, если мы толкаем частицу равномерно, она должна тормозиться жидкостью с силой, пропорциональной скорости. Кроме инерции жидкости, существует еще сопротивление течению, вызванное вязкостью и сложным строением жидкости. Для возникновения флуктуа­ции абсолютно необходимо существование необратимых потерь, нечто вроде сопротивления. Пока таких потерь нет, нет способа получить kT '. Причина флуктуации тесно связана с такими потерями. Мы еще обсудим, каков механизм такого трения, мы поговорим о силах, пропорциональных скорости, и выясним, откуда они берутся. А пока давайте просто предположим, что такое сопротивление существует. Тогда формула для движения под действием внешней силы, если она толкает частицу самым обычным способом, выглядит