Feynmann - Feynmann 1

Предположим, что мы умножили вектор а на число а. Что нужно понимать под таким произведением? Договоримся по­нимать под этим вектор с компонентами аа х , аа у , aa z . Дока­жите сами, что это действительно вектор.

Рассмотрим теперь вычитание векторов. Можно определить вычитание тем же способом, что и сложение, но вместо того, чтобы складывать, будем вычитать составляющие. Можно также определить вычитание как сложение с отрицательным вектором -b=(-1)b. Результат будет тот же.

Вычитание векторов показано на фиг. 11.5.

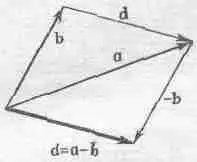
Фиг. 11,5 . Вычитание векторов.

На этом черте­же изображено

d= а- b= а+(- b); заметим также, что, зная векторы аи b, разность а- bможно легко найти из эквивалентного соотношения а= b+d. Таким образом найти раз­ность векторов даже легче, чем сумму: просто нужно провести вектор, соединяющий bи а, и вы получите а- b!

Перейдем теперь к скорости. Почему скорость есть вектор? Если координаты точки равны х, у, z , то скорость ее равна dx / dt , dy / dt , dz / dt . Вектор это или не вектор? Дифференцируя выражение (11.5), можно найти закон преобразования dx ' ldt . Видно, что величины dx / dt , dy / dt преобразуются по тому же закону, что и х и у. Таким образом, скорость есть вектор. Вы­ражение для скорости можно записать очень интересно:

v =dr/dt.

Постараемся нагляднее представить себе, что такое ско­рость и почему она вектор. Далеко ли продвинется частица за малое время Dt? Ответ: на Dr, т. е. если частица находится «здесь» в первое мгновение, а «там» — во второе, то векторная разность положений частицы равна вектору Dr=r 2-r 1. расположенному вдоль направления движения. Как это выглядит, показано на фиг. 11.6. Если разделить этот вектор на промежуток времени Dt = t 2 - t 1 , то мы получим вектор «средней скорости».

Иначе говоря, под вектором скорости мы понимаем предел разности радиус-векторов, соответствующих моментам t+Dt и t , деленной на Dt при Dt, стремящемся к нулю:

Скорость есть вектор постольку, поскольку она равна разности двух векторов. Это верно также и потому, что составляющие этого вектора равны dx / dt , dy / dt , dz / dt . Подумав над тем, что сейчас было проделано, мы придем к выводу, что, продиффе­ренцировав любой вектор по времени, мы снова получим какой-то новый вектор. Таким образом, имеется несколько способов получать новые векторы: 1) умножая вектор на постоянное число; 2) дифференцируя вектор по времени; 3) складывая два вектора или вычитая.

§ 6. Законы Ньютона в векторной записи

Чтобы записать законы Ньютона в векторной форме, мы должны поучиться еще кое-чему и определить вектор ускоре­ния. Этот вектор равен производной по времени вектора скоро­сти, причем легко показать, что его составляющие равны вто­рым производным х, у и z no t :

После этого законы Ньютона можно записать таким образом: или ma = F, (11.13)

m(d 2r/dt 2)=F (11.14)

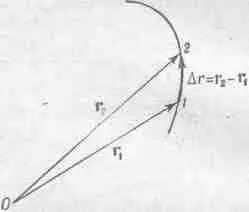
Фиг. 11.6. Перемещение частиц за малое время Dt=t 2-t 1,.

Теперь задача о доказательстве инвариантности законов Нью­тона относительно вращений сводится к следующему: нужно доказать, что а (ускорение) есть вектор; это мы уже сделали. Затем нужно доказать, что F (сила) есть вектор; это мы предпола­гаем. Следовательно, если сила есть вектор, то уравнение (11.13) будет выглядеть одинаково во всех системах координат, ибо нам известно, что ускорение тоже вектор. Запись уравнений в виде, не содержащем явно х, у, z , привлекательна тем, что нам нет необходимости выписывать три уравнения каждый раз, ког­да мы хотим написать законы Ньютона или другие законы фи­зики. Мы записываем то, что выглядит как один закон, хотя фактически, конечно, это три закона для каждой оси системы координат, потому что любое векторное уравнение содержит в себе утверждение, что все составляющие равны.