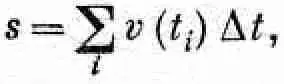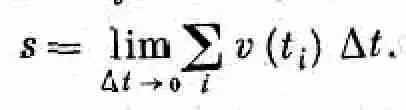Feynmann - Feynmann 1

s + Ds= A(t + Dt) 2+ В (t+ Dt) + С =At 3+Bt+С+ЗAt 2Dt+ВDt+3At (Dt) 2+A(Dt) 3

а

s=At 3 +Bt+C,

то Ds=3At 2Dt+BDt+3At(Dt) 2+A(Dt) 3.

Но нам нужна не сама величина Ds, а отношение Ds/Dt. После деления на Dt получим выражение

D s / D t = 3 At s +В + 3 At (Dt)+A(Dt) 3, которое после устремления Dt к нулю превратится в

Ds/Dt=3'At 2+B.

В этом состоит процесс взятия производной, или дифференциро­вания функций. На самом деле он несколько легче, чем это ка­жется на первый взгляд. Заметьте, что если в разложениях, по­добных предыдущим, встречаются члены, пропорциональные (Dt) 2или (Dt) 3или еще более высоким степеням, то их можно сразу вычеркнуть, поскольку они все равно обратятся в нуль, когда в конце мы будем Dt устремлять к нулю. После небольшой тренировки вы сразу будете видеть, что нужно оставлять, а что сразу отбрасывать. Существует много правил и формул для дифференцирования различных видов функций. Их можно либо запомнить, либо пользоваться специальными таблицами. Небольшой список таких правил приводится в табл. 8,3.

Таблица 8.3 · некоторые производные

s, u, v , w — произвольные функции;

а, b , с, n — произвольные постоянные.

§ 4. Расстояние как интеграл

Обсудим теперь обратную проблему. Пусть вместо таблицы расстояний нам дана таблица скоростей в различные моменты времени, начиная с нуля. В табл. 8.4 представлена зависимость скорости падающего шара от времени. Аналогичную таблицу можно составить и для машины, если записывать показания спидометра через каждую минуту или полминуты. Но можно ли, зная скорость машины в любой момент времени, вычислить расстояние, которое ею было пройдено?

Таблица 8.4 · скорость падающего шара

Эта задача обратна той, которую мы только что рассмотрели. Как же решить ее, если скорость машины непостоянна, если она то ускоряется до 90 км/час, то замедляется, затем где-то останавливается у свето­фора и т.д.? Сделать это нетрудно. Нужно использовать ту же идею и выражать полное расстояние через бесконечно малые его части. Пусть в первую секунду скорость будет v 1 , тогда по формуле Ds = v 1Dt можно вычислить расстояние, пройденное за эту секунду. В следующую секунду скорость будет несколько другой, хотя, может быть, и близкой к первоначальной, а расстояние, пройденное машиной за вторую секунду, будет равно новой скорости, умноженной на интервал времени (1 сек). Этот процесс можно продолжить дальше, до самого конца пути. В ре­зультате мы получим много маленьких отрезков, которые в сум­ме дадут весь путь. Таким образом, путь является суммой ско­ростей, умноженных на отдельные интервалы времени, или s = SvDt, где греческая буква S (сигма) означает сумми­рование. Точнее, это будет сумма скоростей в некоторые мо­менты времени, скажем t i , умноженные на Dt:

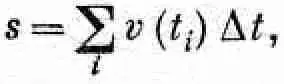
(8.6)

причем каждый последующий момент t i +1 находится по пра­вилу t i +1=t i+Dt. Но расстояние, полученное этим методом, не будет точным, поскольку скорость за время Dt все же изменяет­ся. Выход из этого положения заключается в том, чтобы брать все меньшие и меньшие интервалы Dt , т. е. разбивать время дви­жения на все большее число все меньших отрезков. В конце концов мы придем к следующему, теперь уже точному выра­жению для пройденного пути:

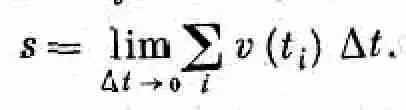
(8.7)

Математики придумали для этого предела, как и для диф­ференциала, специальный символ. Значок D превращается в d, напоминая о том, что интервал времени сколь угодно мал, а знак суммирования превращается в ∫ — искаженное большое S , первая буква латинского слова «Summa». Этот значок назван интегралом. Таким образом, мы пишем

s=∫v(t)dt, (8.8)

где v ( t ) — скорость в момент t . Сама же операция суммирования этих членов называется интегрированием. Она противополож­на операции дифференцирования в том смысле, что производная этого интеграла равна v ( t ), так что один оператор ( d / dt ) «уничто­жает» другой (∫). Это дает возможность получать фор­мулы для интегралов путем обращения формул для дифферен­циалов: интеграл от функции, стоящей в правой колонке табл.8.3, будет равен функции, стоящей в левой колонке. Диф­ференцируя все виды функций, вы сами можете составить таблицу интегралов.