Unknown - ТЕХНИКА БЫСТРОГО ЧТЕНИЯ

Логика психофизических исследований привела к материалистическому объяснению “магии” числа семь. И не даром число семь часто есть в народных пословицах и поговорках. “Один с сошкой, семеро с ложкой”; “Семь раз примерь, один раз отрежь” и т. д., в русских народных сказках и в сказках других народов мира. С детства всем памятна сказка “Про репку”. В этой сказке семь персонажей: репка, бабка, дедка, внучка, Жучка, кошка, мышка.

Исследования В. Я. Проппа, изучившего 100 русских сказок, показали, что, различаясь по сюжету, все они однотипны по своему количественному и качественному составу участников: их всегда семь — вредитель, даритель, помощник, царевна (или ее отец), отравитель, герой, ложный герой. Видимо, фольклорное искусство также подчинялось общим законам человеческого восприятия.

Исследователи, изучающие закономерности развития языка и мышления, отмечают, что все языки мира имеют тенденцию к оптимизации объема словаря, исходя из конкретных возможностей механизмов мозга, а не из фактического многообразия структуры окружающего мира.

“По-видимому, — пишет Дж. Миллер, — наш организм имеет какой-то предел, ограничивающий наши способности воспринимать информацию и обусловленный в свою очередь либо процессом научения, либо самим строением нашей нервной системы”.

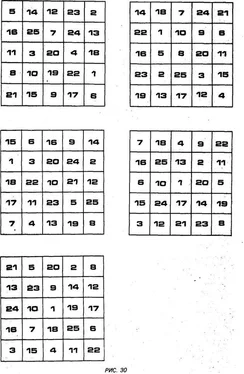
Теперь, представьте себе, что испытуемому, поочередно показывают листы бумаги с различным числом нанесенных на них символов, например точек. Если число этих знаков не превышает семи, человек, не считая, сразу, интуитивно называет верное число: происходит так называемое мгновенное схватывание, или, как говорят психологи, симультанное восприятие (иногда его называют объемом восприятия). Заметим, что хотя и в первом (акустическом) и во втором (зрительном) опытах мы получили одно и то же оптимизированное число семь, процессы, лежащие в их основе, могут быть и различными. Таким образом, эта универсальная закономерность определяет только объем непосредственного восприятия, который оценивается семью элементами. Как было установлено Дж. Миллером в последующих экспериментах, при восприятии имеет значение именно общее число элементарных блоков информации, а не их содержание. Иначе говоря, объем оперативного восприятия зависит по существу не от количества суммарной информации, а от числа группировок блоков символов, или “кусков” информации, — оно (это число) постоянно и равно 7± 2. Это правило имеет большое значение и для быстрого чтения. В самом деле, если число одномоментно воспринимаемых “кусков” информации структурно постоянно, то для повышения эффективности чтения нужно сделать их содержание более емким. Например, если рассмотреть три объекта: восемь цифр, семь букв и шесть слов, то их количественные характеристики почти одинаковы. Однако их информационная емкость весьма различна. Так, восемь цифр несут информацию, равную только 26 битам, семь букв — 35 битам, шесть слов — 84 битам. Тем не менее, по правилу Миллера эти объекты запоминаются почти одинаково.

Значит, при равноодинаковом восприятии человек получает в словах больше информации, чем в буквах, и в предложениях больше, чем в словах. Иначе говоря, при чтении мозг органичней воспринимает тем больше информации, чем выше абстрагирующий уровень кода передачи информации. Способность выполнять такое перекодирование по типовым алгоритмам вместо того, чтобы хранить миллиарды частных случаев, когда встречается то или иное явление, — главная особенность системы человеческой памяти.

Кодировать информацию можно цифрами, словами, предложениями и даже текстами и идеями. Очевидно, наибольшее количество информации передается кодом идей, этот код самый емкий и экономичный.

Из этого следует второй промежуточный вывод: для повышения эффективности восприятия и запоминания текста при чтении необходимо объединить считываемую информацию в крупные информативно-смысловые блоки (словосочетания, предложения, идеи). Значит, быстрое чтение, повышая скорость, вместе с тем обеспечивает и высокое качество ее усвоения при правильной организации этого процесса.

Изложенное позволяет разработать методические приемы для обучения быстрому чтению. Суть этих приемов, очевидно, в том, чтобы выработать рациональные способы перекодирования исходного текста с учетом указанной выше закономерности Миллера.

Здесь нужно вспомнить, что уже одно из первых упражнений методики быстрого чтения помогает решить эту задачу. В самом деле: семь блоков интегрального алгоритма чтения есть не что иное, как надежное средство укрупнения считываемой информации, основанное на рассмотренной закономерности 7±2.