Льюис Кэрролл - Льюис Кэрролл - Досуги математические и не только (ЛП)

Для других столетий требуется учесть напоминание Доджсона по учёту високосных годов среди годов с двумя нулями (так называемое солнечное уравнение). В своей модифицированной версии Конвей предлагает следующую таблицу для годов нашей эры (новый стиль):

Тогда Судный день для 1811 года находится суммированием 1800 + 11 + 4 = 5 + 11 + 2 = 4 mod 7.

Названная книга Роуза Болла и поныне чрезвычайно популярна. Существует даже её перевод на русский язык ( Болл У., Коксетер Г. Математические эссе и развлечения. М., «Мир», 1986). Однако и на русском языке, и в западных переизданиях эта некогда весьма пёстрая книга теперь существует в уменьшенной наполовину, если не на две трети, редакции, идущей от десятого прижизненного издания, в дальнейшем редактируемого известным математиком Г. Коксетером (так, указанный русский перевод сделан с 12-го коксетеровского издания!). То место, на которое ссылается Доджсон, ныне в книге отсутствует. Приведём соответствующий отрывок по четвёртому авторскому изданию.

«Пусть m и n — это числа, определённые как показано ниже.

(1) Разделить число, обозначающее год, на 4, на 7 и на 19, а соответствующие остатки от деления нацело обозначить как a , b и c .

(2) Разделить 19 с + m на 30 и остаток обозначить через d .

(3) Разделить 2 a + 4 b + 6 d + n на 7 и остаток обозначить через e .

(4) Тогда пасхальное полнолуние состоится через d дней после 21 марта, и Пасха выпадет на (22 + d + e )-е число марта либо на ( d + e – 9)-й день апреля, за исключением случая, когда расчёт даст 29 для d и 6 для e (как получается для 1981-го года), — в этом случае Пасха приходится на 19-е апреля вместо 26-го; и за исключением случая, когда расчёт даст 28 для d , 6 для e и при этом c > 10 (как получается для 1954-го года) — тогда Пасха приходится на 18-е апреля вместо 25-го, и таким образом в этих двух случаях Пасха наступает на неделю раньше того срока, который получается согласно настоящему правилу.

Юлианский календарь свободен от подобных исключений, в григорианском же они появляются, правда очень редко (cм. прим. [23] — А. М. )

Остаётся только установить значения m и n для конкретного периода. В юлианском календаре имеем m = 15, n = 6. В григорианском календаре

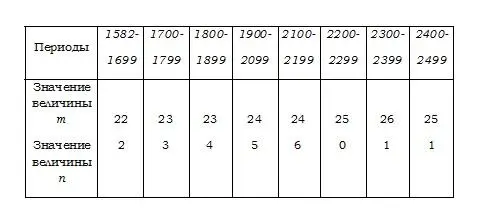
Так, для года 1908 имеем m = 24, n = 5; следовательно, a = 0, b = 4, c = 8, d = 26, а e = 2 и пасхальное воскресенье приходится на 19-е апреля. После 4200-го года вид настоящего правила должен быть слегка видоизменён. <���…>

Можно избегнуть необходимости запоминать значения m и n , если учесть, что если N — данный год, а { N / x } обозначает целую часть отношения N к x , то m есть остаток от деления 15 + ξ на 30, а n есть остаток от деления 6 + η на 7; здесь для юлианского календаря ξ = 0, η = 0, тогда как для григорианского календаря

ξ = { N /100} – { N /400} – { N /300}, η = { N /100} – { N /400} – 2.

Если мы примем эти значения для m и n и если положим для a , b , c их значения, а именно,

a = N – 4{N/4}, b = N – 7{N/7}, c = N – 19{N/19},

то наше правило примет следующий вид. Разделить 19 N – { N /19} +15 + ξ на 30 и обозначить остаток как d . Затем разделить 6( N + d + 1) – { N /19} + η на 7 и обозначить остаток как e . Тогда пасхальное полнолуние выпадет на d -й день после 21-го марта, а Пасха, соответственно, придётся на (22 + d + e )-й день марта либо на ( d + e – 9)-е число апреля; исключение составляют случаи, когда расчёт даёт 29 для d и 6 для e или же 28 для d и 6 для e с тем, что c > 10, когда Пасха приходится на ( d + e – 16)-й день апреля.

Так, если N = 1899, делим 19(1899) – 99 + 15 + (18 – 4 – 6) на 30, что даёт d = 5; продолжаем делением 6(1899 + 5 + 1) – 474 + (18 – 4 – 2) на 7, что даёт e = 6; а потому Пасха придётся на 2-е апреля».

То есть, остаток при делении 4325 на семь равняется 6. В следующих примерах этого пункта он равняется соответственно 4 и 2. Далее — аналогично.

Дефектом числа (либо фигуры) называется количественное отличие данного числа (либо параметров данной фигуры) от некоторого определённого числа (либо определённых параметров фигур данного класса; так, дефектом треугольника называется отличие суммы углов данного треугольника от 180°).