Льюис Кэрролл - Льюис Кэрролл - Досуги математические и не только (ЛП)

Основная идея данного способа пришла мне в голову 19 сентября 1879 года. Я размышлял над большим неудобством, возникающим при обычной процедуре умножения в столбик из-за того, что две цифры, которые требуется перемножить, часто находятся друг от друга на большом расстоянии, и о том преимуществе, каким стала бы возможность записать задачу так, чтобы все такие цифры оказывались стоящими рядом. Тогда и появилась счастливая мысль, что если написать меньшее число задом наперёд и передвигать его поверх другого числа вдоль него, то на каждом этапе такого смещения мы получим наблюдаемый непосредственно набор из пар цифр, чьи произведения потребуется только сложить друг с другом, чтобы получить единственный столбец для действия над ним уже как обычно [1].

Способ, который я вывел из этой идеи, может быть изложен следующим образом.

Записать два данных числа так, чтобы меньшее, если они неравной длины, располагалось над большим, а их разряды единиц были совмещены по вертикали. Провести под нашими числами черту. На отдельной полоске бумаги записать верхнее число задом наперёд , пометив сверху его разряд единиц. Прикрыть этой полоской бумаги верхнее из наших чисел, совместив разряды единиц [чисел, оставшихся видимыми,] по вертикали. Обозрев эту пару цифр, записать цифру разряда единиц их произведения прямо под чертой и по вертикали с меткой, а цифру разряда десятков — ещё ниже и на одну позицию левее. Сместить полоску на одну позицию влево. Обозрев две пары цифр, которые выстроились по вертикали теперь, просуммировать их произведения, начиная с той пары, что стоит правее, и записать цифру разряда единиц результата прямо под чертой и по вертикали с меткой, а цифру разряда десятков ещё ниже и на одну позицию левее. Снова сместить полоску и действовать как ранее.

Конкретный пример прояснит дело. Пусть даны числа 574 и 3891. Запишем их, как здесь показано, проведём снизу черту и запишем число 574 на отдельной полоске бумаги, поставив метку поверх цифры 4.

Прикроем нашей полоской верхнее число, так чтобы метка оказалась прямо над разрядом единиц нижнего числа.

Обозрев располагающуюся вертикально пару цифр, говорим: «36» и вписываем цифру 6 под чертой и вертикально с меткой, а цифру 3 ещё ниже и на одну позицию левее.

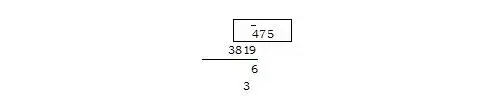
Смещаем полоску бумаги на одну позицию влево.

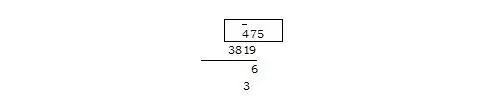
Обозрев две располагающиеся вертикально пары цифр, говорим: «63 и 4 будет 67». Вписываем 7 и 6.

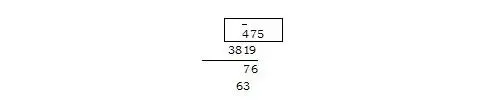
Смещаем полоску бумаги на одну позицию влево.

Обозрев три располагающиеся вертикально пары цифр, говорим: «45 и 7 будет 52, да 32 будет 84». Вписываем 4 и 8.

Смещаем полоску как ранее.

Обозрев три располагающиеся вертикально пары цифр, говорим: «5 и 56 будет 61, да 12 будет 73». Вписываем 3 и 7.

Смещаем полоску как ранее.

Обозрев две располагающиеся вертикально пары цифр, говорим: «40 и 21 будет 61». Вписываем 1 и 6.

Смещаем полоску как ранее.

Обозрев вертикальную пару цифр, говорим: «15». Вписываем 5 и 1.

Теперь удаляем полоску бумаги, проводим внизу черту и складываем вместе две полученные строки.

Читатель заметит, что действие при каждой позиции нашей полоски бумаги — вещь совершенно обособленная, осуществляемая сама по себе безотносительно к остальной части решения. Следовательно, при возникновении сомнения насчёт какой-либо отдельной цифры в ответе, те цифры, суммой которых она является, могут быть проверены сами по себе ; например, если у нас есть подозрение, что цифра 9 неверна, мы можем проверить цифру 7, стоящую прямо над ней, помещая полоску бумаги в позицию восьмого этапа наших выкладок, а затем и цифру 1, стоящую над 7, поместив полоску в позицию десятого этапа.