Льюис Кэрролл - Льюис Кэрролл - Досуги математические и не только (ЛП)

Когда верхнее из двух данных чисел содержит не более четырёх или пяти цифр, действовать согласно вышеизложенному Правилу сравнительно легко, но при по-настоящему длинном верхнем числе окажется удобным проходить каждый ряд произведений дважды — первый раз суммируя их разряды единиц и занося разряд единиц результата в верхнюю строку решения, а затем суммируя их разряды десятков. Так, ход рассуждения для шестого этапа может быть следующим: «5 и 7 будет 12, да 2 будет 14». Заносим 4, 1 в уме. «5 и 3 будет 8». Вписываем 8 [2].

При действии по такому видоизменённому способу в голове рождается следующее Правило.

Собирая разряды единиц набора произведений пар цифр, помнить, что если один из членов пары равен 1, то разряд единиц равен другому [члену пары]; если один [из них] равен 5, то разряд единиц будет 5 либо 0 соответственно тому, чётным или нечётным будет другой ; если один [из них] равен 9, разряд единиц равен 10 минус другой .

Собирая десятки, помнить, что если один из членов пары равен 1 или если сумма двух членов меньше 7, то разряд десятков отсутствует ; если один [из членов пары] равен 5, то разряд десятков равен количеству двоек, содержащихся в другом ; если один [из них] есть 9, то разряд десятков равен другому минус 1.

Во многих случаях такие задачи на умножение длинных чисел требуют суммирования только двух строк [под чертой]; когда же появляется набор произведений, чья сумма содержит три цифры, возникает нужда в третьей строке; когда сумма набора произведений содержит четыре цифры — то в четвёртой , но такое возникает только в том случае, когда меньшее из чисел содержит по меньшей мере тринадцать цифр; а когда сумма произведений содержит пять цифр — нужен пятый ряд, но такое происходит, лишь если меньшее число содержит по крайней мере сто двадцать четыре цифры, а потому превышает триллион секстиллионов!

Данный способ легко приложим и к перемножению десятичных дробей; нужно лишь для начала поместить полоску бумаги так, чтобы метка пришлась строго по вертикали над тем разрядом десятичных, на который требуется перенести действие. Я приведу здесь два примера, выделив из хода решения каждого, во-первых, сам пример в его исходной записи; во-вторых, стадию прямо перед тем, как полоска будет смещена первый раз; в-третьих, конечное состояние — перед тем как полоска будет убрана; и в-четвёртых, итог складывания.

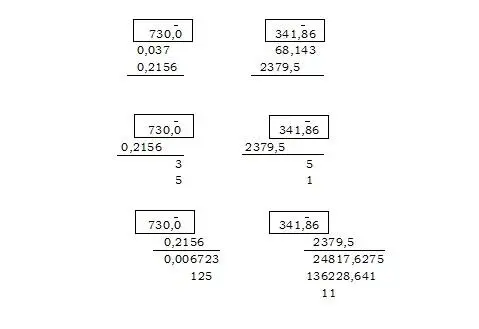
Следовательно, ответ в первом примере будет 0,0080 с точностью до четвёртого знака; во втором примере ответ, с точностью до второго знака, будет 16211446,27.

§1. Делитель вида (10 n ± 1) [3]

Год назад я обнаружил один любопытный [4]факт: если поставить «0» над разрядом единиц некоторого данного числа, которому случится быть кратным 9, и вычесть во всю длину, всякий раз ставя разность над следующей цифрой, то конечное вычитание даст 0 в остатке, а верхний ряд, по отбрасывании его конечного нуля, оказывается «частным-9» данного числа (то есть, частным от деления данного числа на 9).

Обнаружив этот факт, я тот час пришёл, по аналогии, к открытию того, что если поставить 0 под разрядом единиц некоторого данного числа, которому случится быть кратным 11, и действовать подобным образом, мы придём к подобному же результату.

В каждом случае я получал частное от деления столбиком более коротким и простым способом вычитания ; но поскольку к этому результату можно было придти лишь в том (сравнительно редком) случае, когда данное число оказывалось точным кратным 9 или 11, это открытие виделось более любопытным, чем полезным.

Позднее я стал рассматривать случаи, когда данное число не было точным кратным. Я нашёл, что конечное вычитание при этом приносило некоторое число, иногда сразу являвшееся действительным остатком, получаемым от деления, но в любом случае дающее заготовку для нахождения такого остатка. Но поскольку оно не приносило частного (кроме как посредством некоторой весьма «экстравагантной» процедуры, значительно более длинной и трудоёмкой, чем подлинное деление), это открытие также не подлежало практическому применению.

Но совсем недавно мне пришло на ум выяснить, что будет, если после нахождения остатка поместить этот последний вместо того нуля над или под разрядом единиц, а затем вычесть как ранее. Меня поразило открытие того факта, что прежний результат повторился: конечное вычитание принесло 0 в остатке, а новая строка, по отбрасывании её разряда единиц, оказалась требуемым частным.