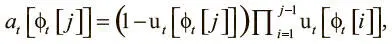
где j ∈ 1,…, N .
На первый взгляд, уравнение кажется непонятным. Его проще осознать, если взять числовой пример. Пусть u t = [1, 0.7, 0.2, 0.4]. Расчеты вы сможете провести сами. В итоге у вас должно получиться такое взвешивание выделения: a t = [0, 0.024, 0.8, 0.12]. После вычислений становится ясно, как работает формула: 1 − u t [ϕ t [ j ]] делает вес ячейки пропорциональным степени ее незанятости. Отметим, что произведение 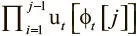 становится все меньше при итерациях по свободному списку, поскольку мы постоянно перемножаем числа из множества от 0 до 1. Оно дополнительно снижает вес ячейки при переходе от наименее используемой ячейки к наиболее используемой. В результате самая свободная ячейка получает наибольший вес, а самая занятая — наименьший. Так мы можем гарантировать способность сосредоточиваться на одной ячейке, не рассчитывая, что модель научится этому с нуля: отсюда большая надежность и сокращение времени обучения.
становится все меньше при итерациях по свободному списку, поскольку мы постоянно перемножаем числа из множества от 0 до 1. Оно дополнительно снижает вес ячейки при переходе от наименее используемой ячейки к наиболее используемой. В результате самая свободная ячейка получает наибольший вес, а самая занятая — наименьший. Так мы можем гарантировать способность сосредоточиваться на одной ячейке, не рассчитывая, что модель научится этому с нуля: отсюда большая надежность и сокращение времени обучения.
Имея взвешивание выделения a t и взвешивание просмотра 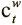 , которые мы получаем из механизма адресации по содержанию:
, которые мы получаем из механизма адресации по содержанию: 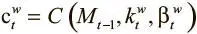 , где
, где 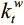 ,
, 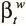 — ключ и сила просмотра, полученные по вектору интерфейса, можно вывести итоговое взвешивание записи:
— ключ и сила просмотра, полученные по вектору интерфейса, можно вывести итоговое взвешивание записи:
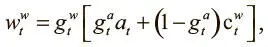
где 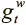 ,
, 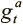 — значения от 0 до 1, именуемые вентилем записи и вентилем выделения, которые мы тоже получаем из контроллера через вектор интерфейса. Вентили контролируют операцию записи, причем
— значения от 0 до 1, именуемые вентилем записи и вентилем выделения, которые мы тоже получаем из контроллера через вектор интерфейса. Вентили контролируют операцию записи, причем 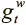 сначала определяет, должна ли вообще делаться запись, а
сначала определяет, должна ли вообще делаться запись, а 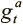 показывает, будем ли мы добавлять информацию в новую ячейку при помощи взвешивания выделения или изменим текущее значение, указанное просмотровым взвешиванием.
показывает, будем ли мы добавлять информацию в новую ячейку при помощи взвешивания выделения или изменим текущее значение, указанное просмотровым взвешиванием.
Повторное использование памяти в DNC
А если при вычислении взвешивания выделения обнаружится, что все ячейки используются, то есть u t = 1? Тогда все взвешивания обратятся в 0 и в память не поступят новые данные. Потому-то необходимо уметь освобождать и заново использовать память.
Чтобы знать, какие ячейки можно освободить, а какие нет, строим вектор удержания ψ t размера N , который указывает, какое количество данных в каждой ячейке следует сохранить. Каждый элемент принимает значение от 0 до 1, где 0 указывает, что ячейка может быть освобождена, а 1 — что она должна быть полностью сохранена. Вектор вычисляется так:
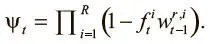
Уравнение сообщает, что уровень, до которого ячейку следует освободить, пропорционален тому, сколько данных прочтено из нее на последних нескольких шагах разными головками (представлены значениями взвешиваний 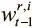 ). Но постоянное освобождение ячейки памяти сразу после чтения ее данных нежелательно, поскольку эти данные могут нам понадобиться позже.
). Но постоянное освобождение ячейки памяти сразу после чтения ее данных нежелательно, поскольку эти данные могут нам понадобиться позже.
Оставим контроллеру возможность решить, когда освобождать, а когда сохранять ячейку после прочтения, выдавая набор из R свободных вентилей  , значения которых составляют от 0 до 1. Это определяет, насколько нужно освобождать ячейки, на основе того, что их только что прочли. Контроллер обучается использованию этих вентилей для достижения желаемого поведения. Как только вектор удержания получен, можно с его помощью обновить вектор использования, чтобы отражать все освобождения и сохранения:
, значения которых составляют от 0 до 1. Это определяет, насколько нужно освобождать ячейки, на основе того, что их только что прочли. Контроллер обучается использованию этих вентилей для достижения желаемого поведения. Как только вектор удержания получен, можно с его помощью обновить вектор использования, чтобы отражать все освобождения и сохранения:
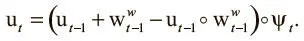
Это уравнение можно прочесть так: ячейка будет использована, если она была сохранена (ее значение ψ t ≈ 1) и либо уже в работе, либо в нее только что произведена запись (о чем свидетельствует значение 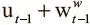 ). Вычитание поэлементного произведения
). Вычитание поэлементного произведения 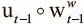 возвращает выражение в диапазон между 0 и 1, значение использования вновь становится действительным (если взвешивание записи при предыдущем использовании вышло за пределы 1).
возвращает выражение в диапазон между 0 и 1, значение использования вновь становится действительным (если взвешивание записи при предыдущем использовании вышло за пределы 1).
Читать дальше
Конец ознакомительного отрывка
Купить книгу

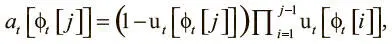
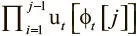 становится все меньше при итерациях по свободному списку, поскольку мы постоянно перемножаем числа из множества от 0 до 1. Оно дополнительно снижает вес ячейки при переходе от наименее используемой ячейки к наиболее используемой. В результате самая свободная ячейка получает наибольший вес, а самая занятая — наименьший. Так мы можем гарантировать способность сосредоточиваться на одной ячейке, не рассчитывая, что модель научится этому с нуля: отсюда большая надежность и сокращение времени обучения.
становится все меньше при итерациях по свободному списку, поскольку мы постоянно перемножаем числа из множества от 0 до 1. Оно дополнительно снижает вес ячейки при переходе от наименее используемой ячейки к наиболее используемой. В результате самая свободная ячейка получает наибольший вес, а самая занятая — наименьший. Так мы можем гарантировать способность сосредоточиваться на одной ячейке, не рассчитывая, что модель научится этому с нуля: отсюда большая надежность и сокращение времени обучения.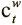 , которые мы получаем из механизма адресации по содержанию:
, которые мы получаем из механизма адресации по содержанию: 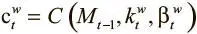 , где
, где 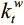 ,
, 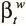 — ключ и сила просмотра, полученные по вектору интерфейса, можно вывести итоговое взвешивание записи:
— ключ и сила просмотра, полученные по вектору интерфейса, можно вывести итоговое взвешивание записи: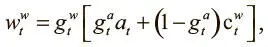
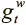 ,
, 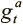 — значения от 0 до 1, именуемые вентилем записи и вентилем выделения, которые мы тоже получаем из контроллера через вектор интерфейса. Вентили контролируют операцию записи, причем
— значения от 0 до 1, именуемые вентилем записи и вентилем выделения, которые мы тоже получаем из контроллера через вектор интерфейса. Вентили контролируют операцию записи, причем 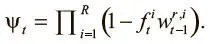
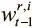 ). Но постоянное освобождение ячейки памяти сразу после чтения ее данных нежелательно, поскольку эти данные могут нам понадобиться позже.
). Но постоянное освобождение ячейки памяти сразу после чтения ее данных нежелательно, поскольку эти данные могут нам понадобиться позже. , значения которых составляют от 0 до 1. Это определяет, насколько нужно освобождать ячейки, на основе того, что их только что прочли. Контроллер обучается использованию этих вентилей для достижения желаемого поведения. Как только вектор удержания получен, можно с его помощью обновить вектор использования, чтобы отражать все освобождения и сохранения:
, значения которых составляют от 0 до 1. Это определяет, насколько нужно освобождать ячейки, на основе того, что их только что прочли. Контроллер обучается использованию этих вентилей для достижения желаемого поведения. Как только вектор удержания получен, можно с его помощью обновить вектор использования, чтобы отражать все освобождения и сохранения: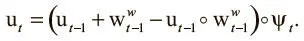
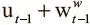 ). Вычитание поэлементного произведения
). Вычитание поэлементного произведения 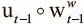 возвращает выражение в диапазон между 0 и 1, значение использования вновь становится действительным (если взвешивание записи при предыдущем использовании вышло за пределы 1).
возвращает выражение в диапазон между 0 и 1, значение использования вновь становится действительным (если взвешивание записи при предыдущем использовании вышло за пределы 1).










