Дуглас Хаббард - Как измерить все, что угодно [Оценка стоимости нематериального в бизнесе]

В нашем примере с магазином автозапчастей покупатель, заявивший «да, я еще сюда вернусь», — это попадание, а размер выборки — это число попыток. Используя биноминальное распределение, менеджер может определить вероятность конкретного результата, например вероятность того, что среди 20 выбранных нами покупателей вернутся в магазин только 14, хотя вообще таких людей должно быть 90 %. В Excel мы запишем: =binomdist(14, 20, 0,9, 0), что даст нам 88,7-процентную вероятность 14 попаданий при 20 случайно выбранных покупателях, если бы на самом деле 90 % посетителей сказали, что готовы сделать еще одну покупку. Отсюда мы уже видим, что верхняя граница нашего первоначального диапазона не слишком правдоподобна.

Предположим теперь, что мы рассчитали эту вероятность для генеральной совокупности, в которой доля повторных покупателей составит сначала 75 %, затем 76, 77 и т. д. вплоть до 90 % (таким образом, шаг равен 1 %). Используя некоторые таблицы в программе Excel, мы сможем быстро рассчитать вероятность конкретного результата при данном «истинном» проценте повторных покупателей. Для каждого приращения на 1 % получим вероятность того, что 14 из 20 покупателей ответят утвердительно на вопрос о возвращении за повторной покупкой при данном «истинном» проценте повторных покупателей. Я бы рассчитывал эти вероятности для каждого приращения на 1 %, начиная от 60 % (что с учетом нашего 90-процентного CI маловероятно, но возможно) и заканчивая 100 %. Для каждого приращения проведем расчет на основе теоремы Байеса. Запишем все это вместе в следующем виде:

P(Prop = Х|Попадания = 14/20) = P(Prop = X) × Р(Попадания = 14/20|Prop = X) / Р(Попадания = 14/20),

где

P(Prop = Х|Попадания = 14/20) — вероятность данного процента повторных покупателей в генеральной совокупности (процента X) при условии, что 14 из 20 случайно отобранных объектов являются попаданиями;

P(Prop = X) — вероятность того, что определенный процент покупателей в генеральной совокупности вернется снова (например, X = 90 % генеральной совокупности покупателей, которые действительно сказали, что вернутся снова);

P(Попадания = 14/20|Prop = X) — вероятность 14 попаданий из 20 случайно выбранных объектов при данном проценте (проценте X) повторных покупателей в генеральной совокупности;

P(Попадания = 14/20) — вероятность получения 14 попаданий из 20 попыток при условии, что все возможные проценты повторных покупателей в генеральной совокупности находятся в первоначальном диапазоне.

Мы знаем, как рассчитать Р(Попадания = 14/20|Prop = 90 %) в Excel: [=binomdist(14, 20, 0,9, 1)]. Теперь нам нужно придумать, как рассчитать P(Prop = X) и Р(Попадания = 14/20). Мы можем рассчитать вероятность каждого приращения на 1 % доли повторных покупателей в нашем диапазоне, вернувшись снова к функции =normdist() в Excel и используя калиброванную оценку. Например, чтобы получить вероятность того, что 78–79 % наших покупателей окажутся повторными (или, по крайней мере, заявят об этом во время опроса), мы можем записать следующую формулу Excel:

=normdist(0,79, 0,825, 0,0456, 1) — normdist(0,78, 0,825, 0,0456, 1).

Число 0,825 — это среднее значение нашего калиброванного диапазона: (75 % + 90 %)/2; 0,0456 — среднее квадратичное отклонение (как вы помните, в 90-процентном CI 3,29 среднего квадратичного отклонения): (90 % — 75 %)/3,29. Формула normdist дает нам разность между вероятностью получить менее 79 % и вероятностью получить менее 78 %, которая составляет 5,95 %. Мы можем определить это для каждого приращения на 1 % в исходном диапазоне, а затем рассчитать вероятность того, что доля повторных покупателей в генеральной совокупности равна X [то есть P(Prop = X)] для каждого мало-мальски вероятного значения X в нашем диапазоне.

Расчет значения P(Попадания = 14/20) основан на всем, что мы делали до сих пор. Чтобы рассчитать P(Y), когда мы знаем P(Y|X) и P(X) для каждого значения X, суммируем произведения P(Y|X) × P(X) для каждого X. Зная, как рассчитать P(Попадания = 14/20|Prop = X) и P(Prop = X) для любого X, мы просто умножаем эти две величины для каждого X, затем суммируем их и получаем, что P(Попадания = 14/20) = 8,56 %.

Теперь для каждого значения в исходном диапазоне (и даже немного за его пределами, чтобы получить «хвосты» в уравнении) мы рассчитываем P(Prop = X), P(Попадания = 14/20|Prop = X) и P(Prop = X |Попадания = 14/20), для каждого приращения на 1 % повторных покупателей в генеральной совокупности величина P(Попадания = 14/20) для всех одинакова и равна 8,56 % (см. табл. 10.1).

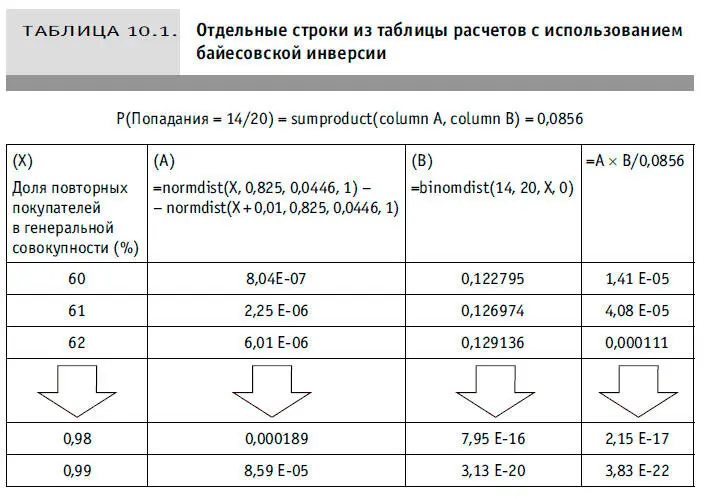
Значения в последнем столбце — вероятности данного процента повторных покупателей в их генеральной совокупности. Если суммировать накопленные значения в последнем столбце (складываем все предшествующие значения в строке), то выяснится, что итог составит около 5 %, когда процент повторных покупателей достигнет 79 %, и 95 %, когда этот процент будет равен 85 %. Это означает, что наш новый 90-процентный CI сократится до 79–85 %. Это не слишком большое сужение первоначального диапазона (75–90 %), но тем не менее достаточно информативное. Теперь, согласно накопленным значениям последнего столбца, вероятность того, что мы находимся ниже основного порога в 80 %, составляет 61 %. Эту электронную таблицу целиком можно найти на веб-сайте: www.howtomeasureanything.com