Отметим, что уравнение 6–3 может быть подставлено в уравнение 6–4 и далее в уравнение 6–5; тогда получим:
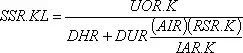 .
.
6-6, R
Таким образом, могут быть исключены вспомогательные уравнения, а темп выражен только через уровни и константы.
В главе 13 уравнения 6–3, 6–4 и 6–5 рассматриваются применительно к обстановке на промышленном предприятии. Каждое из этих вспомогательных уравнений определяет имеющую самостоятельный смысл переменную, важную для отражения системы. Наши представления о системе были бы безнадежно затемнены, если бы мы действительно производили подстановку, выполненную в уравнении 6–6.
Вспомогательная переменная в принципе зависит только от уже известных уровней и от других вспомогательных переменных, значения которых могут быть вычислены до того, как они понадобятся. Как отмечалось в отношении уравнений темпов, значения темпов, относящиеся к предшествующему интервалу времени JK, могут быть иногда использованы во вспомогательных уравнениях; хотя это, строго говоря, неверно, однако при определенных условиях такой метод может дать достаточно хорошее приближение к средним значениям, получаемым для коротких интервалов времени.
Дополнительные уравнения.Дополнительные уравнения применяются при определении переменных, не являющихся частью структуры модели, но используемых при печати и графическом изображении величин, представляющих интерес для понимания поведения модели. Мы можем пожелать собрать информацию (например, о сумме запасов в целой системе), которая не используется в процессе выработки какого-либо решения в модели. Обозначение « S » указывает на дополнительное уравнение.
Уравнения начальных условий. Уравнения начальных условий используются для определения исходных значений всех уровней (и некоторых темпов), которое должно быть произведено до начала первого цикла решения уравнений. Они также используются в начальный момент времени для вычисления значений одних констант, исходя из значений других. Уравнения начальных условий решаются только один раз перед началом каждого проигрывания модели. Обозначение « N » указывает на уравнение начальных условий.
Интервал решений должен быть достаточно коротким, чтобы его величина не влияла сколько-нибудь серьезно на результаты вычислений. Его следует выбирать по возможности максимально большим с тем, чтобы не допускать увеличения загрузки вычислительной машины там, где это не вызвано необходимостью.
Основное требование ограничения продолжительности интервала вытекает из характера построения системы уравнений. Уровни определяют темпы, а темпы определяют уровни, но система уравнений является «открытой»; под этим подразумевается, что каналы обратной связи остаются в течение интервала решений DT закрытыми. Поэтому интервал должен быть достаточно коротким, чтобы изменения в уровнях между моментами решений не привели к недопустимой дискретности темпов.
В большинстве наших систем допустимый интервал между вычислениями будет определяться запаздываниями, имеющими форму показательной функции (см. главу 8). Как мы увидим, интервал обязательно должен быть меньше продолжительности любого запаздывания первого порядка; желательно, чтобы он был меньше его половины. Поскольку запаздывания третьего порядка наиболее употребительны и поскольку они эквивалентны трем последовательным запаздываниям первого порядка, каждое из которых составляет одну треть запаздывания третьего порядка, интервал решений должен быть меньше одной шестой общей продолжительности самого короткого запаздывания третьего порядка в рассматриваемой системе.
Сформулированное правило является эмпирическим. Наилучший способ проверки правильности выбора интервала решений состоит в варьировании его величины и наблюдении за влиянием ее на результаты вычислений.
Особым критерием, определяющим максимально допустимую величину интервала решений, является взаимосвязь между значениями уровней и темпами потоков, входящих в эти уровни и исходящих из них. Интервал решений должен быть достаточно коротким, чтобы суммарный входящий или исходящий поток не вызывал больших изменений в содержании уровня за один интервал решений. Например, если возможен высокий темп исходящего потока при небольшой величине содержимого в уровне, то интервал решений должен быть достаточно коротким с тем, чтобы только часть содержимого уровня могла быть исчерпана за один интервал решений. Если интервал настолько велик, что на его протяжении из уровня может быть изъято содержимое в большем количестве, чем имелось в нем в начале интервала, то в конце интервала содержимое уровня будет выражаться отрицательной величиной, что не имеет смысла.
Читать дальше

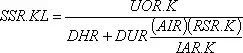 .
.






![Джей Джей Барридж - Секрет рапторов [litres]](/books/420944/dzhej-dzhej-barridzh-sekret-raptorov-litres-thumb.webp)



