Примером уравнения темпа может служить уравнение запаздывания исходящего потока, имеющее вид показательной функции первого порядка. Объяснение уравнения будет дано в главе 8, здесь же мы рассмотрим лишь его форму:
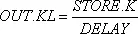 ,
,
6.2, R
где
OUT — темп исходящего потока (единицы в неделю);
STORE — количество, находящееся в настоящее время в запаздывании (единицы);
DELAY — константа, средняя продолжительность времени, необходимого для преодоления запаздывания (недели).
Это второе наше уравнение представляет собой уравнение темпа, о чем свидетельствует буква « R » в его шифре. Уравнение определяет величину темпа « OUT » и показывает, какое значение он будет иметь на протяжении следующего интервала времени KL. Темп должен быть равен величине уровня «STORE» в настоящий момент К, деленной на константу, названную «DELAY» (без какого-либо обозначения времени, поскольку это константа). Ко времени решения уравнения количественные значения для STORE и DELAY должны быть, конечно, известными.
Вспомогательные уравнения.Уравнение темпа может нередко стать очень сложным, если его действительно формулировать лишь на основе одних уровней, как это утверждалось до сих пор. К тому же темп может быть часто лучше определен, если пользоваться одним или несколькими понятиями, имеющими самостоятельный смысл и характеризуемыми в свою очередь уровнями системы. Часто бывает удобно разбить уравнение темпа на отдельные части, которые мы будем называть вспомогательными уравнениями. Вспомогательное уравнение оказывает большую помощь при решении задачи приведения модели в полное соответствие с действительной системой, так как с его помощью можно определить в отдельности многие факторы, принимаемые в расчет при выработке решения.
Вспомогательные уравнения являются промежуточными; они могут быть подставлены одно в другое (если имеется несколько «слоев» вспомогательных уравнений) и далее — в уравнения темпов [39] Подстановка не повышает «порядок» уравнений, поскольку результирующее уравнение темпа по-прежнему содержит в себе лишь информацию, полученную из данных об уровнях на момент времени К.
. Путем алгебраической подстановки вспомогательные переменные могут быть исключены из уравнений, что достигается ценой увеличения сложности уравнений темпов и потери в то же время простоты и ясности значения отдельных уравнений модели.
Вспомогательные уравнения решаются на момент времени К после решения уравнений уровней, поскольку для решения вспомогательных уравнений, как и для решения уравнений темпов, часть которых они собой представляют, используются данные о значениях уровней в тот же момент времени. Они должны быть решены прежде уравнений темпов, поскольку получаемые при этом результаты необходимы для подстановки в уравнения темпов.
В отличие от уравнений темпов и уровней вспомогательные уравнения нельзя решать в произвольной последовательности, так как одни вспомогательные уравнения могут быть составными частями других, а два или более вспомогательных уравнений могут образовывать «цепочку», которая должна решаться в определенном порядке таким образом, чтобы решение одного уравнения могло быть использовано при решении последующих. Если формулировка уравнений правильна, то должна существовать возможность такой последовательной подстановки. Система вспомогательных уравнений не должна быть замкнутой; это указывало бы на недопустимую и ненужную формулировку уравнений.
Ниже показана цепь из двух вспомогательных уравнений между двумя уровнями и уравнением темпа:
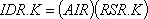 ,
,
6-3, A
где RSR — уровень, a AIR — константа,
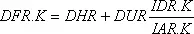 ,
,
6–4,
А
где IAR — уровень, a DHR и DUR — константы,
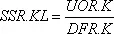 ,
,
6-5, R
где UOR — уровень.
Следует заметить, что в уравнении 6–3, А (индекс « A » применяется в шифре вспомогательных уравнений) уровень RSR в момент времени К используется в качестве ввода для вспомогательной переменной IDR в момент времени К- Выражения AIR, DHR и DUR — константы. В тот же момент времени К, IDR является вместе с другим уровнем вводом для вспомогательной переменной DFR. В свою очередь DFR используется вместе с другим уровнем в уравнении темпа 6–5,R для определения темпа SSR.
Читать дальше

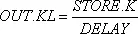 ,
,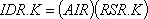 ,
,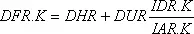 ,
,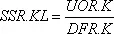 ,
,






![Джей Джей Барридж - Секрет рапторов [litres]](/books/420944/dzhej-dzhej-barridzh-sekret-raptorov-litres-thumb.webp)



