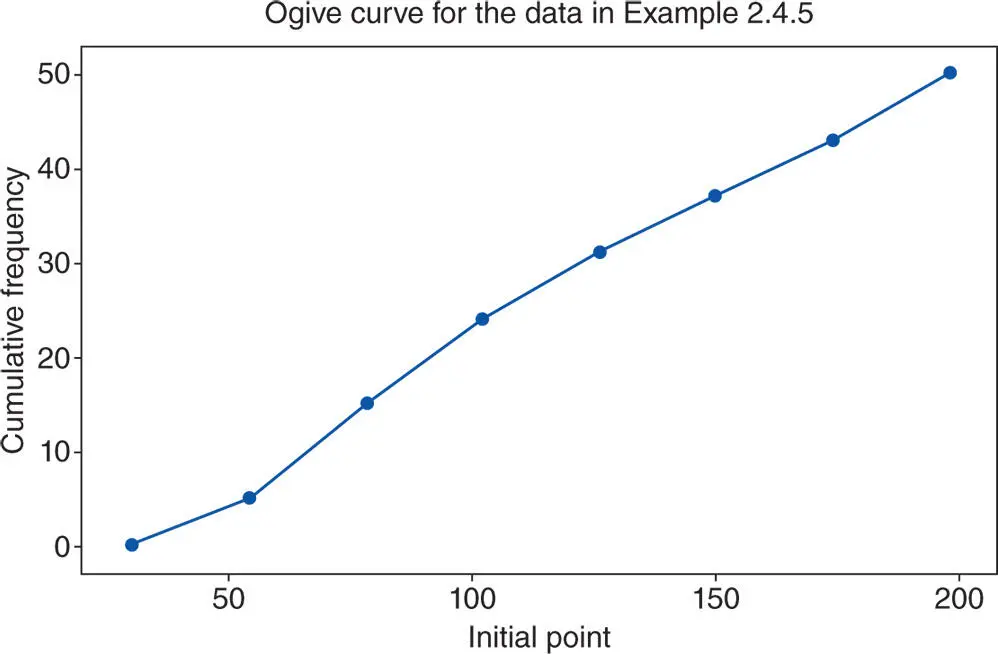
Figure 2.4.11Ogive curve using MINITAB for the data in Example 2.4.5.
A line graph, also known as a time‐series graph, is commonly used to study any trends in the variable of interest that might occur over time. In a line graph, time is marked on the horizontal axis (the 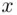 ‐axis) and the variable on the vertical axis (the
‐axis) and the variable on the vertical axis (the  ‐axis). For illustration, we use the data of Table 2.4.4given below in Example 2.4.6.
‐axis). For illustration, we use the data of Table 2.4.4given below in Example 2.4.6.
Example 2.4.6(Lawn mowers) The data in Table 2.4.4 give the number of lawn mowers sold by a garden shop over a period of 12 months of a given year. Prepare a line graph for these data.
Table 2.4.4Lawn mowers sold by a garden shop over a period of 12 months of a given year.
| Months |
January |
February |
March |
April |
May |
June |
July |
August |
September |
October |
November |
December |
| LM sold |
2 |
1 |
4 |
10 |
57 |
62 |
64 |
68 |
40 |
15 |
10 |
5 |
Solution:To prepare the line graph, plot the data in Table 2.4.4using the 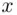 ‐axis for the months and the
‐axis for the months and the 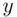 ‐axis for the lawn mowers sold, and then join the plotted points with a freehand curve. The line graph for the data in this example is as shown in Figure 2.4.12, which was created using MINITAB ( Graph
‐axis for the lawn mowers sold, and then join the plotted points with a freehand curve. The line graph for the data in this example is as shown in Figure 2.4.12, which was created using MINITAB ( Graph 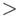 Time Series Plot).
Time Series Plot).
From the line graph in Figure 2.4.12, we can see that the sale of lawn mowers is seasonal, since more mowers were sold in the summer months. Another point worth noting is that a good number of lawn mowers were sold in September when summer is winding down. This may be explained by the fact that many stores want to clear out such items as the mowing season is about to end, and many customers take advantage of clearance sales. Any mower sales during winter months may result because of a discounted price, or perhaps the store may be located where winters are very mild, and there is still a need for mowers, but at a much lower rate.
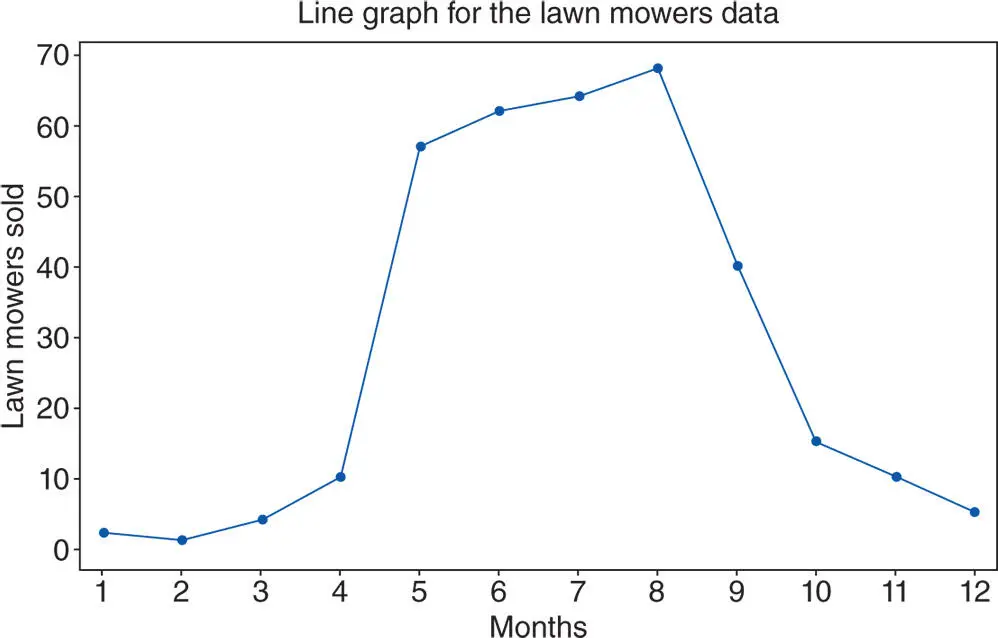
Figure 2.4.12Line graph for the data on lawn mowers in Example 2.4.6.
Before discussing this plot, we need the concept of the median of a set of data. The median is the value, say  , that divides the data into two equal parts when the data are arranged in ascending order. A working definition is the following (a more detailed examination and discussion of the median is given in Section 2.5.1).
, that divides the data into two equal parts when the data are arranged in ascending order. A working definition is the following (a more detailed examination and discussion of the median is given in Section 2.5.1).
Suppose that we have a set of values, obtained by measuring a certain variable, say  times. Then, the median of these data, say
times. Then, the median of these data, say 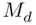 , is the value of the variable that satisfies the following two conditions:
, is the value of the variable that satisfies the following two conditions:
1 at most 50% of the values in the set are less than , and
2 at most 50% of the values in the set are greater than .
We now turn our attention to the stem‐and‐leaf plot invented by John Tukey. This plot is a graphical tool used to display quantitative data. Each data value is split into two parts, the part with leading digits is called the stem , and the rest is called the leaf . Thus, for example, the data value 5.15 is divided in two parts with 5 for a stem and 15 for a leaf.
A stem‐and‐leaf plot is a powerful tool used to summarize quantitative data. The stem‐and‐leaf plot has numerous advantages over both the frequency distribution table and the frequency histogram. One major advantage of the stem‐and‐leaf plot over the frequency distribution table is that from a frequency distribution table, we cannot retrieve the original data, whereas from a stem‐and‐leaf plot, we can easily retrieve the data in its original form. In other words, if we use the information from a stem‐and‐leaf plot, there is no loss of information, but this is not true of the frequency distribution table. We illustrate the construction of the stem‐and‐leaf plot with the following example.
Example 2.4.7(Spare parts supply) A manufacturing company has been awarded a huge contract by the Defense Department to supply spare parts. In order to provide these parts on schedule, the company needs to hire a large number of new workers. To estimate how many workers to hire, representatives of the Human Resources Department decided to take a random sample of 80 workers and find the number of parts each worker produces per week. The data collected is given in Table 2.4.5. Prepare a stem‐and‐leaf diagram for these data.
Table 2.4.5 Number of parts produced per week by each worker.
| 73 |
70 |
68 |
79 |
84 |
85 |
77 |
75 |
61 |
69 |
74 |
80 |
83 |
82 |
86 |
87 |
78 |
81 |
68 |
71 |
| 74 |
73 |
69 |
68 |
87 |
85 |
86 |
87 |
89 |
90 |
92 |
71 |
93 |
67 |
66 |
65 |
68 |
73 |
72 |
83 |
| 76 |
74 |
89 |
86 |
91 |
92 |
65 |
64 |
62 |
67 |
63 |
69 |
73 |
69 |
71 |
76 |
77 |
84 |
83 |
85 |
| 81 |
87 |
93 |
92 |
81 |
80 |
70 |
63 |
65 |
62 |
69 |
74 |
76 |
83 |
85 |
91 |
89 |
90 |
85 |
82 |
Solution:The stem‐and‐leaf plot for the data in Table 2.4.5is as shown in Figure 2.4.13.
The first column in Figure 2.4.13gives the cumulative frequency starting from the top and from the bottom of the column but ending at the stem that lies before the stem containing the median. The number in parentheses indicates the stem that contains the median value of the data, and the frequency of that stem.

Figure 2.4.13Stem‐and‐leaf plot for the data in Example 2.4.7with increment 10.

Figure 2.4.14Stem‐and‐leaf plot for the data in Example 2.4.7with increment 5.
Читать дальше


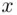 ‐axis) and the variable on the vertical axis (the
‐axis) and the variable on the vertical axis (the  ‐axis). For illustration, we use the data of Table 2.4.4given below in Example 2.4.6.
‐axis). For illustration, we use the data of Table 2.4.4given below in Example 2.4.6.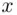 ‐axis for the months and the
‐axis for the months and the 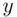 ‐axis for the lawn mowers sold, and then join the plotted points with a freehand curve. The line graph for the data in this example is as shown in Figure 2.4.12, which was created using MINITAB ( Graph
‐axis for the lawn mowers sold, and then join the plotted points with a freehand curve. The line graph for the data in this example is as shown in Figure 2.4.12, which was created using MINITAB ( Graph  Time Series Plot).
Time Series Plot).
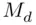 , that divides the data into two equal parts when the data are arranged in ascending order. A working definition is the following (a more detailed examination and discussion of the median is given in Section 2.5.1).
, that divides the data into two equal parts when the data are arranged in ascending order. A working definition is the following (a more detailed examination and discussion of the median is given in Section 2.5.1).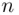 times. Then, the median of these data, say
times. Then, the median of these data, say 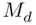 , is the value of the variable that satisfies the following two conditions:
, is the value of the variable that satisfies the following two conditions:












