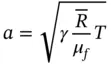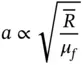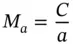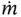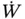If there is no energy addition, storage, or loss between sections 1 and 2, the energy will be conserved, and E 1= E 2:
(1.28) 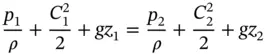
or, in terms of pressure heads (in metres, for example)
(1.29) 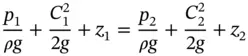
If both sides of Eq. (1.28) are multiplied by ρ , it can be rewritten in terms of fluid pressure as
(1.30) 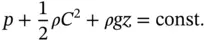
Equation (1.30) is known as Bernoulli's equation. If it is rewritten in differential form, it gives Euler's equation:
(1.31) 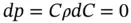
1.2.2.1 General Energy Equation
If there is energy addition, storage, or loss between sections 1 and 2 in Figure 1.6, the energy equation can be written as
(1.32) 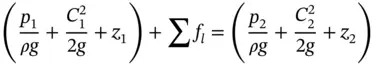
where ∑ f lis the algebraic sum of all losses and gains between points 1 and 2. These could include mechanical energy gained from a booster pump, mechanical energy lost by running a fluid motor or turbine, and energy lost due to friction in the control volume.
1.2.3 Acoustic Velocity (Speed of Sound)
The acoustic velocity of a fluid is the speed of sound in the fluid under isentropic conditions and is given by
(1.33) 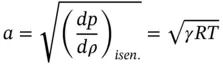
For a gas of molecular mass μ f, 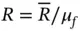 , where
, where 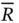 is the universal gas constant (=8314.4 J / kmole K ).
is the universal gas constant (=8314.4 J / kmole K ).
Rewriting Eq. (1.33) in terms of the universal gas constant 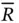 ,
,
(1.34) 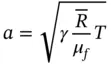
At a given temperature and ratio of specific heats, the acoustic velocity can be written as
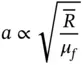
The Mach number M a(in honour of Ernst Mach) is defined as
(1.35) 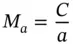
The Mach number is used to indicate speed of flow or forward speed of aircraft and rockets and also to indicate different flow regimes:
| Mach number |
Flow regime |
| M a< 1 |
Subsonic flow |
| M a= 1 |
Sonic flow |
| 1 < M a< 5 |
Supersonic flow |
| M a> 5 |
Hypersonic flow |
1.2.4 Similitude and Dimensional Analysis
Many problems in fluid mechanics can be solved analytically; however, in a large number of cases, problems can only be solved by experimentation. Similitude and dimensional analysis make it possible to use measurements obtained in a laboratory under specific conditions to describe the behaviour of other similar systems without the need for further experimentation.
1.2.4.1 Dimensional Analysis
Dimensional analysis is based on representing physical quantities with a combination of fundamental dimensions, noting that units of two sides of an equation must be consistent.
In fluid mechanics, as in other branches of engineering sciences, the fundamental dimensions are mass ( M ), length ( L ), and time ( T ). Temperature, if applicable, can be assigned a fundamental dimension such as ( θ ). These fundamental dimensions can be used to provide qualitative descriptions of physical quantities: for example, velocity can be described as LT −1, density as MT −3, and so on. Table 1.2lists the symbols, units, and dimensions of common physical quantities. For effective application of dimensional analysis, it is essential to state which independent variables are relevant to the problem.
Table 1.2Symbols, units, and dimensions of common physical quantities.
| Quantity |
Symbol |
Units |
Dimensions |
| Length |
l |
m |
L |
| Time |
t |
s |
T |
| Mass |
m |
kg |
M |
| Force |
F |
N |
MLT −2 |
| Temperature |
T |
K |
θ |
| Velocity |
C or V |
m / s |
LT −1 |
| Volume |
m 3 |
m 3 |
L 3 |
| Acceleration |
a |
m / s 2 |
LT −2 |
| Angular velocity |
ω |
rad |
T −1 |
| Area |
m 2 |
m 2 |
L 2 |
| Volume flow rate |
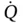 |
m 3/ s |
L 3 T −1 |
| Mass flow rate |
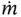 |
kg / s |
MT −1 |
| Pressure |
p |
N / m 2 |
ML −1 T −2 |
| Density |
ρ |
kg / m 3 |
ML −3 |
| Specific weight |
γ |
N / m 3 |
ML −2 T −2 |
| Dynamic viscosity |
μ |
N . s / m 2 |
ML −1 T −1 |
| Kinematic viscosity |
ν |
m 2/ s |
L 2 T −1 |
| Work |
W |
J |
ML 2 T −2 |
| Power |
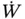 |
W |
ML 2 T −3 |
| Surface tension |
σ |
N / m |
MT −2 |
| Bulk modulus |
B |
N / m 2 |
ML −1 T −2 |
| Momentum |
G |
kg . m / s |
MLT −1 |
| Torque, moment of force |
T , M |
N . m |
ML 2 T −2 |
In cases where temperature is a basic physical quantity and it is preferable to avoid using an extra fundamental dimension such as θ , the gas constant is usually lumped together with the temperature, and the combined variable RT = p / ρ (from the equation of state) will have the dimensions
Читать дальше

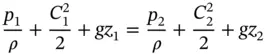
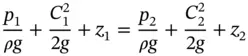
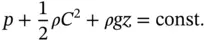
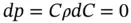
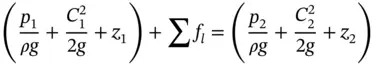
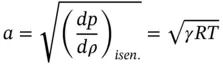
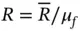 , where
, where 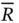 is the universal gas constant (=8314.4 J / kmole K ).
is the universal gas constant (=8314.4 J / kmole K ).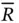 ,
,