4 Unequal slots. Consider a generalization of a frame, which consists of a header, followed by communication resources. However, now assume that the communication resources are not organized into equal slots and instead the frame can contain slots with different lengths. Discuss how does this affect the type and amount of signaling bits used in the header.
5 Reservation with variable number of data slots. The analysis in Section 1.4.3is done for the case in which the number of data slots following the reservation slots is fixed. Let us now consider the case in which is variable and adapted to the actual number of resources required in the reservation slots. Assume that each of the devices can request up to resources through the reservation packets.Find the number of bits that are required in the reservation packets and the allocation packet.Using the assumptions for bit duration from Section 1.4.3, find the maximal throughput that can be offered in a given frame. NB: the maximal throughput depends on the amount of resources requested by the devices.In practical systems, the allocation packet A may not be received by some of the devices due to errors caused by noise or interference. When is the impact of not receiving A worse, when is fixed or when is variable? How do you suggest to design the system to be more robust to this type of error?
1 1The term broadcast outside of information theory is used to denote the message that is sent to all devices within the range. In that sense, the term multicast is used when the message is sent to a subset of two or more devices within the range. Hence, in this sense a broadcast is a special case of multicast. On the other hand, broadcast in an information-theoretic sense means that the transmission of a device is received by multiple devices, regardless of who the intended receiver of the message is. Thus, we can say that a transmission over a wireless medium is a broadcast, but the actual message sent may be intended as a unicast to a specific device or multicast to a group of devices.
2 2Here we conservatively assume that a device sends a reservation packet even if it has no data to send.

2 Random Access: How to Talk in Crowded Dark Room
In the previous chapter, the dark room analogy was used to introduce the problem addressed by rendezvous protocols. Thinking about the same analogy, let us assume that Basil is in a dark room and some of the other people in the room want to talk to him. Basil cannot use visual cues, such as a raised hand, in order to schedule who should speak at him at a given time. Furthermore, the room is crowded, there are many other people in it, but only a few of them are active, in the sense that they want to say something to Basil at a given time instant. With this in mind, it is clearly not efficient to ask the people one by one if they have something to say, as most of them will be just silent and thus most of the time will be spent inefficiently. This observation paves the way for random access protocols , in which the reservation slots or data transmission slots are not exclusively pre-allocated to a device. The attribute “random” comes from the fact that the decision to transmit is randomized. The randomness can be caused by random packet arrival to the device. Alternatively, when the packet is already in the buffer of the device, the device can make a deliberate randomized choice to transmit or not. The dark room reflects the fact that we need to use the same wireless medium both to obtain the right to transmit data, which is a form of metadata , and to send the actual data.
Similar to the rendezvous protocol, random access is an indispensable solution when the devices need to perform an initial access . The objective of the initial access is to connect a device to the base station Basil, potentially going through a process of authentication, allocation of a temporary short address, etc. Clearly, in the case of initial access there are many, potentially infinite, number of devices that can connect, but at a given time only one or very few of them want to do that. After the initial access, the communication can either proceed as a scheduled one or, if the activity of the device is sporadic, rely again on a random access. The latter is typical for scenarios in which a massive number of small Internet of Things (IoT) devices are connected to a base station Basil. However, at a given time only a small subset of them is active; this subset is random and unknown to Basil.
The canonical scenario for random access is depicted in Figure 2.1. In this scenario, a number of uncoordinated mobile devices attempt to transmit data or control information to a common receiver.
In presenting the algorithms for random access we will keep the assumptions on the collision model established in the previous chapter: a packet is an atomic transmission unit and any overlap between two or more packets leads to collision and incorrect reception of all collided packets. We will consider two classes of random access protocols: ALOHA type and probing (also known as tree type protocols). The variant of ALOHA considered here is not the original ALOHA, but rather framed ALOHA, a variant that logically extends the reservation schemes discussed in the previous chapter.
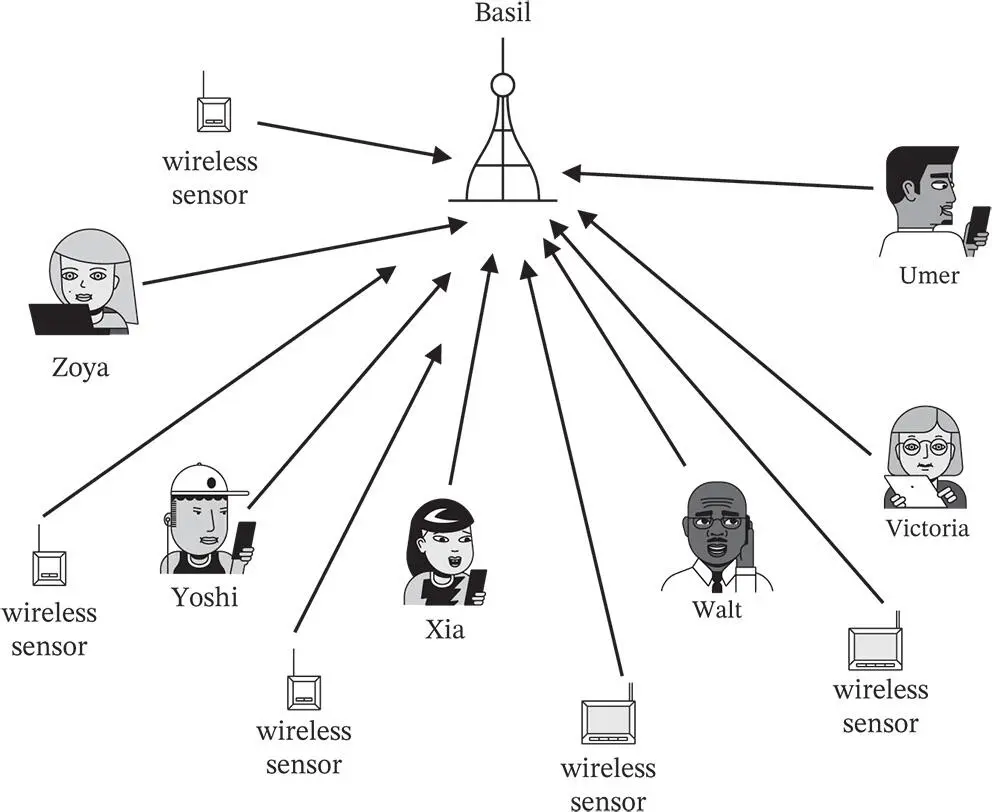 Figure 2.1 Canonical scenario for random access protocols, where a number of uncoordinated devices attempt to transmit in the uplink to the same receiver, which here is the base station Basil.
Figure 2.1 Canonical scenario for random access protocols, where a number of uncoordinated devices attempt to transmit in the uplink to the same receiver, which here is the base station Basil.
The context for this discussion is in Section 1.4.3, where we introduced the reservation slots. Looking only at the expression (1.8), we can try to understand in which situation the usage of reservation slots may not lead to an efficient operation. For example, let us take the scenario in which the terminals connected to Basil are not phones, but sensors that monitor certain physical phenomena and only occasionally have data to send.
The parameters of this scenario can be described as follows. The total number of sensors 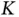 connected to Basil is large, while the number of users that have some data to send at a given frame is small. In other words, the probability that a particular sensor has data to send in a particular frame is very low. The amount of data
connected to Basil is large, while the number of users that have some data to send at a given frame is small. In other words, the probability that a particular sensor has data to send in a particular frame is very low. The amount of data 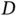 in a packet of each sensor is also small. Let us assume that the number
in a packet of each sensor is also small. Let us assume that the number 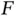 of data slots that follow the reservation slots is small and, furthermore, all
of data slots that follow the reservation slots is small and, furthermore, all 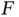 slots are full with data. In that case, using the equation (1.8), one can see that
slots are full with data. In that case, using the equation (1.8), one can see that 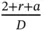 starts to dominate in the denominator, leading to decrease in the goodput. This is an example of a case in which the resources consumed by the metadata, which include reservation slots and all the other auxiliary packets, become comparable to the amount of data that needs to be sent and the overall system efficiency drops.
starts to dominate in the denominator, leading to decrease in the goodput. This is an example of a case in which the resources consumed by the metadata, which include reservation slots and all the other auxiliary packets, become comparable to the amount of data that needs to be sent and the overall system efficiency drops.
Читать дальше


 Figure 2.1 Canonical scenario for random access protocols, where a number of uncoordinated devices attempt to transmit in the uplink to the same receiver, which here is the base station Basil.
Figure 2.1 Canonical scenario for random access protocols, where a number of uncoordinated devices attempt to transmit in the uplink to the same receiver, which here is the base station Basil.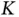 connected to Basil is large, while the number of users that have some data to send at a given frame is small. In other words, the probability that a particular sensor has data to send in a particular frame is very low. The amount of data
connected to Basil is large, while the number of users that have some data to send at a given frame is small. In other words, the probability that a particular sensor has data to send in a particular frame is very low. The amount of data 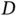 in a packet of each sensor is also small. Let us assume that the number
in a packet of each sensor is also small. Let us assume that the number 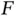 of data slots that follow the reservation slots is small and, furthermore, all
of data slots that follow the reservation slots is small and, furthermore, all 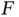 slots are full with data. In that case, using the equation (1.8), one can see that
slots are full with data. In that case, using the equation (1.8), one can see that 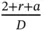 starts to dominate in the denominator, leading to decrease in the goodput. This is an example of a case in which the resources consumed by the metadata, which include reservation slots and all the other auxiliary packets, become comparable to the amount of data that needs to be sent and the overall system efficiency drops.
starts to dominate in the denominator, leading to decrease in the goodput. This is an example of a case in which the resources consumed by the metadata, which include reservation slots and all the other auxiliary packets, become comparable to the amount of data that needs to be sent and the overall system efficiency drops.










