In the extreme case there is only 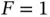 sensor transmitting. Let us fix
sensor transmitting. Let us fix 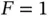 and assume that, in a given frame, the probability that a particular sensor has data to send is
and assume that, in a given frame, the probability that a particular sensor has data to send is 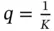 . This means that, on average, only
. This means that, on average, only 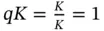 packet comes in a frame from the total population of
packet comes in a frame from the total population of 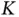 sensors. Let then the number of reservation slots be
sensors. Let then the number of reservation slots be 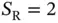 . Recall that, in the previous chapter we had
. Recall that, in the previous chapter we had 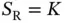 , such that each reservation slot was deterministically and exclusively allocated to a single device (sensor). Here we have
, such that each reservation slot was deterministically and exclusively allocated to a single device (sensor). Here we have 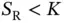 , such that an exclusive allocation is not possible. Let us assume that, at the start of the frame, each sensor that has data to send picks randomly one of the
, such that an exclusive allocation is not possible. Let us assume that, at the start of the frame, each sensor that has data to send picks randomly one of the 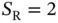 reservation slots and sends a reservation packet. Note that, unlike the case with deterministic allocation of reservation slots from the previous chapter, here Basil cannot know who is the sender unless its address is included in the reservation packet. Although in our example the expected number of sensors with data is
reservation slots and sends a reservation packet. Note that, unlike the case with deterministic allocation of reservation slots from the previous chapter, here Basil cannot know who is the sender unless its address is included in the reservation packet. Although in our example the expected number of sensors with data is 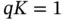 , it can happen, with a significant probability, that two or more sensors have data to send in the same frame. If exactly two out of the
, it can happen, with a significant probability, that two or more sensors have data to send in the same frame. If exactly two out of the 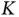 sensors, Zoya and Yoshi, have data to send in the same frame, then the following outcomes are possible:
sensors, Zoya and Yoshi, have data to send in the same frame, then the following outcomes are possible:
1 Case 1. Each sensor picks a different reservation slot. Then Basil receives both reservation packets and decides to allocate the data slot to, for example, Zoya. Yoshi tries again to send its reservation packet in a future frame.
2 Case 2. Both sensors pick the same reservation slot and end up in a collision. Then Basil cannot allocate the data slot to any of the two sensors, leaving the data slot empty.
Each of the two outcomes occurs with probability 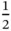 and in both cases it becomes apparent that having a fixed
and in both cases it becomes apparent that having a fixed 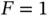 is not efficient. In the first case, the successful reservation of Yoshi is wasted 1 . In the second case, the data transmission slot is empty and wasted, as none of the two sensors can use it for transmission.
is not efficient. In the first case, the successful reservation of Yoshi is wasted 1 . In the second case, the data transmission slot is empty and wasted, as none of the two sensors can use it for transmission.
This leads us to think of a more efficient solution: 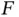 does not need to be fixed, but it would be the best if the value of
does not need to be fixed, but it would be the best if the value of 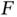 can be adapted to be equal to the number of successful outcomes, denoted by
can be adapted to be equal to the number of successful outcomes, denoted by 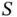 , where
, where 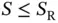 in the reservation frame of size
in the reservation frame of size 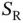 . Basil needs to dynamically set
. Basil needs to dynamically set 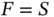 , since in each new frame
, since in each new frame 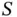 is a random number. Recalling the discussion from the previous chapter, this flexibility demands additional signaling information, as Basil needs to decide the value of
is a random number. Recalling the discussion from the previous chapter, this flexibility demands additional signaling information, as Basil needs to decide the value of 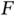 after the reservation phase is finished and then communicate the value
after the reservation phase is finished and then communicate the value 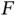 to the terminals. Since there can be at most
to the terminals. Since there can be at most 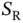 successful reservations, the number of data slots
successful reservations, the number of data slots 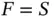 for a frame can range from 0 to
for a frame can range from 0 to 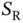 and this number can be specified in the allocation packet, along with the addresses of the devices to which the slots are allocated.
and this number can be specified in the allocation packet, along with the addresses of the devices to which the slots are allocated.
The essence of the described scheme is to allow all the users to randomly access the 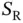 reservation slots. This method of random access is known in the literature as framed ALOHA , as it is a variant of the basic ALOHA protocol. The next question is: how do we choose the number of reservation slots
reservation slots. This method of random access is known in the literature as framed ALOHA , as it is a variant of the basic ALOHA protocol. The next question is: how do we choose the number of reservation slots 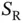 ? We will carry out a quick, non-rigorous analysis, in order to get an insight into the design choices for the described type of system.
? We will carry out a quick, non-rigorous analysis, in order to get an insight into the design choices for the described type of system.
2.1.1 Randomization that Maximizes the ALOHA Throughput
The question of choosing the optimal 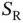 cannot be answered without providing additional elements of the model in which random access is used. To start with, we have not specified the random process that describes the way the sensors attempt to send their packets. The way to model this is to assume a random process that describes whether a sensor device has something to transmit in a given frame. In order to shed light on these issues, we can formulate a simpler problem that is still relevant for making the optimized choice of
cannot be answered without providing additional elements of the model in which random access is used. To start with, we have not specified the random process that describes the way the sensors attempt to send their packets. The way to model this is to assume a random process that describes whether a sensor device has something to transmit in a given frame. In order to shed light on these issues, we can formulate a simpler problem that is still relevant for making the optimized choice of 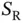 . Let there be
. Let there be 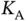 active sensors with data to send among the population of
active sensors with data to send among the population of 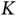 sensors. Each active sensor is trying to send a reservation packet in one of the
sensors. Each active sensor is trying to send a reservation packet in one of the 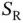 slots. It is important to state that the sensors are not mutually coordinated in any way before starting the random access process.
slots. It is important to state that the sensors are not mutually coordinated in any way before starting the random access process.
Читать дальше

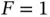 sensor transmitting. Let us fix
sensor transmitting. Let us fix 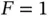 and assume that, in a given frame, the probability that a particular sensor has data to send is
and assume that, in a given frame, the probability that a particular sensor has data to send is 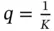 . This means that, on average, only
. This means that, on average, only 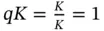 packet comes in a frame from the total population of
packet comes in a frame from the total population of 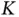 sensors. Let then the number of reservation slots be
sensors. Let then the number of reservation slots be 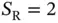 . Recall that, in the previous chapter we had
. Recall that, in the previous chapter we had 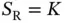 , such that each reservation slot was deterministically and exclusively allocated to a single device (sensor). Here we have
, such that each reservation slot was deterministically and exclusively allocated to a single device (sensor). Here we have 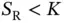 , such that an exclusive allocation is not possible. Let us assume that, at the start of the frame, each sensor that has data to send picks randomly one of the
, such that an exclusive allocation is not possible. Let us assume that, at the start of the frame, each sensor that has data to send picks randomly one of the 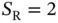 reservation slots and sends a reservation packet. Note that, unlike the case with deterministic allocation of reservation slots from the previous chapter, here Basil cannot know who is the sender unless its address is included in the reservation packet. Although in our example the expected number of sensors with data is
reservation slots and sends a reservation packet. Note that, unlike the case with deterministic allocation of reservation slots from the previous chapter, here Basil cannot know who is the sender unless its address is included in the reservation packet. Although in our example the expected number of sensors with data is 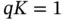 , it can happen, with a significant probability, that two or more sensors have data to send in the same frame. If exactly two out of the
, it can happen, with a significant probability, that two or more sensors have data to send in the same frame. If exactly two out of the 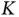 sensors, Zoya and Yoshi, have data to send in the same frame, then the following outcomes are possible:
sensors, Zoya and Yoshi, have data to send in the same frame, then the following outcomes are possible: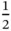 and in both cases it becomes apparent that having a fixed
and in both cases it becomes apparent that having a fixed 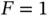 is not efficient. In the first case, the successful reservation of Yoshi is wasted 1 . In the second case, the data transmission slot is empty and wasted, as none of the two sensors can use it for transmission.
is not efficient. In the first case, the successful reservation of Yoshi is wasted 1 . In the second case, the data transmission slot is empty and wasted, as none of the two sensors can use it for transmission.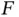 does not need to be fixed, but it would be the best if the value of
does not need to be fixed, but it would be the best if the value of 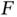 can be adapted to be equal to the number of successful outcomes, denoted by
can be adapted to be equal to the number of successful outcomes, denoted by 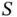 , where
, where 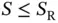 in the reservation frame of size
in the reservation frame of size 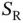 . Basil needs to dynamically set
. Basil needs to dynamically set 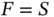 , since in each new frame
, since in each new frame 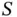 is a random number. Recalling the discussion from the previous chapter, this flexibility demands additional signaling information, as Basil needs to decide the value of
is a random number. Recalling the discussion from the previous chapter, this flexibility demands additional signaling information, as Basil needs to decide the value of 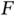 after the reservation phase is finished and then communicate the value
after the reservation phase is finished and then communicate the value 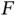 to the terminals. Since there can be at most
to the terminals. Since there can be at most 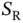 successful reservations, the number of data slots
successful reservations, the number of data slots 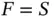 for a frame can range from 0 to
for a frame can range from 0 to 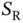 and this number can be specified in the allocation packet, along with the addresses of the devices to which the slots are allocated.
and this number can be specified in the allocation packet, along with the addresses of the devices to which the slots are allocated.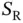 reservation slots. This method of random access is known in the literature as framed ALOHA , as it is a variant of the basic ALOHA protocol. The next question is: how do we choose the number of reservation slots
reservation slots. This method of random access is known in the literature as framed ALOHA , as it is a variant of the basic ALOHA protocol. The next question is: how do we choose the number of reservation slots 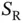 ? We will carry out a quick, non-rigorous analysis, in order to get an insight into the design choices for the described type of system.
? We will carry out a quick, non-rigorous analysis, in order to get an insight into the design choices for the described type of system.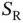 cannot be answered without providing additional elements of the model in which random access is used. To start with, we have not specified the random process that describes the way the sensors attempt to send their packets. The way to model this is to assume a random process that describes whether a sensor device has something to transmit in a given frame. In order to shed light on these issues, we can formulate a simpler problem that is still relevant for making the optimized choice of
cannot be answered without providing additional elements of the model in which random access is used. To start with, we have not specified the random process that describes the way the sensors attempt to send their packets. The way to model this is to assume a random process that describes whether a sensor device has something to transmit in a given frame. In order to shed light on these issues, we can formulate a simpler problem that is still relevant for making the optimized choice of 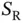 . Let there be
. Let there be 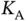 active sensors with data to send among the population of
active sensors with data to send among the population of 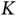 sensors. Each active sensor is trying to send a reservation packet in one of the
sensors. Each active sensor is trying to send a reservation packet in one of the 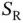 slots. It is important to state that the sensors are not mutually coordinated in any way before starting the random access process.
slots. It is important to state that the sensors are not mutually coordinated in any way before starting the random access process.










