Having said that, there is a certain (dark room) symmetry in the problem: all the sensors look equal to the receiver and each of the 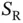 reservation slots looks equal to each sensor. This means that, if a particular sensor Zoya needs to pick a single reservation slot, then each of the reservation slots should have an equal chance to be picked, with probability
reservation slots looks equal to each sensor. This means that, if a particular sensor Zoya needs to pick a single reservation slot, then each of the reservation slots should have an equal chance to be picked, with probability 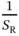 . Considering this, the probability that Zoya will have a successful transmission of her reservation packet in a particular slot is
. Considering this, the probability that Zoya will have a successful transmission of her reservation packet in a particular slot is
(2.1) 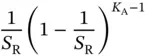
which is the probability that Zoya sends in that slot and that none of the other 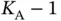 sensors chose it for transmission.
sensors chose it for transmission.
The probability that there is a successful transmission in that slot by any of the 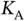 sensors is:
sensors is:
(2.2) 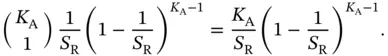
It can be shown that the latter expression is maximized when 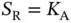 . Hence, the best way is to choose the number of reservation slots to be equal to the number of active sensors that are contending via random access (framed ALOHA), such that the probability of successful reception in a given slot is:
. Hence, the best way is to choose the number of reservation slots to be equal to the number of active sensors that are contending via random access (framed ALOHA), such that the probability of successful reception in a given slot is:
(2.3) 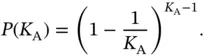
Clearly, this requires knowledge of the number 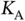 of active sensors in the total population of
of active sensors in the total population of 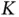 sensors.
sensors.
Let us see the implications that this has on our system. Before the frame starts, Basil knows that there will be 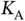 sensors that will be contending with each other in order to request access, but he does not know the identities of these sensors. Note that this is the crucial assumption in the problem setup for random access, since if Basil knows which
sensors that will be contending with each other in order to request access, but he does not know the identities of these sensors. Note that this is the crucial assumption in the problem setup for random access, since if Basil knows which 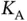 sensors will require access, then there is no need for randomized contention: namely, Basil can simply set
sensors will require access, then there is no need for randomized contention: namely, Basil can simply set 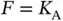 and allocate one data slot to each sensor. Although this observation seems trivial, it is very often overlooked when random access is considered in practical systems. Basil sets
and allocate one data slot to each sensor. Although this observation seems trivial, it is very often overlooked when random access is considered in practical systems. Basil sets 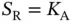 , but the number
, but the number 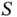 of sensors that successfully send reservation requests is random. This implies that the number of allocated slots
of sensors that successfully send reservation requests is random. This implies that the number of allocated slots 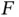 is also random. The expected value of
is also random. The expected value of 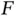 is
is 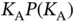 , and one can use (1.8)to calculate the expected goodput in a frame.
, and one can use (1.8)to calculate the expected goodput in a frame.
Another observation is that 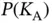 decreases with
decreases with 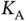 and it reaches
and it reaches 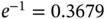 as the number of users goes to infinity. The engineering insight from
as the number of users goes to infinity. The engineering insight from 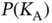 is that, when the users are contending in smaller groups, then the probability of successful transmission experienced by an individual user is higher.
is that, when the users are contending in smaller groups, then the probability of successful transmission experienced by an individual user is higher.
The assumption that Basil knows the exact value of 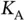 is rather artificial. On the other hand, Basil may know some statistics about the random process according to which the sensors send reservation requests. In that case, it can be reasonable to conclude that Basil knows the expected value of
is rather artificial. On the other hand, Basil may know some statistics about the random process according to which the sensors send reservation requests. In that case, it can be reasonable to conclude that Basil knows the expected value of 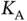 . Although not mathematically rigorous, Basil can work with the expected value as if it is the exact value and use the following approach. At the start of
. Although not mathematically rigorous, Basil can work with the expected value as if it is the exact value and use the following approach. At the start of 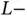 th frame the expected number of sensors that require access, denoted by
th frame the expected number of sensors that require access, denoted by 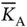 , is given by:
, is given by:
(2.4) 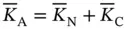
where 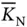 is the expected number of new requests generated from new sensors in the previous,
is the expected number of new requests generated from new sensors in the previous,  th frame.
th frame. 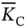 is the expected number of sensors that tried to send request in the previous frames, but did not succeed due to collision. If a frame becomes sufficiently long, then we can apply the law of large numbers, by which the expected values can be approximated as the exact values. For this to be true, the random arrival process of the requests from the sensors should satisfy certain conditions, which we will not discuss in detail here. It suffices to say that, for example, Poisson arrivals of requests over a sufficiently long interval would work. Going back to (2.4), we remove the averaging bar and recast the same equation as
is the expected number of sensors that tried to send request in the previous frames, but did not succeed due to collision. If a frame becomes sufficiently long, then we can apply the law of large numbers, by which the expected values can be approximated as the exact values. For this to be true, the random arrival process of the requests from the sensors should satisfy certain conditions, which we will not discuss in detail here. It suffices to say that, for example, Poisson arrivals of requests over a sufficiently long interval would work. Going back to (2.4), we remove the averaging bar and recast the same equation as 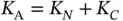 . Using the previous analysis on the probability of successful transmission of a request, we can express
. Using the previous analysis on the probability of successful transmission of a request, we can express 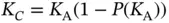 , but since
, but since 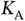 is large, we can write
is large, we can write 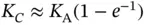 , which leads to:
, which leads to:
Читать дальше

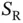 reservation slots looks equal to each sensor. This means that, if a particular sensor Zoya needs to pick a single reservation slot, then each of the reservation slots should have an equal chance to be picked, with probability
reservation slots looks equal to each sensor. This means that, if a particular sensor Zoya needs to pick a single reservation slot, then each of the reservation slots should have an equal chance to be picked, with probability 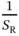 . Considering this, the probability that Zoya will have a successful transmission of her reservation packet in a particular slot is
. Considering this, the probability that Zoya will have a successful transmission of her reservation packet in a particular slot is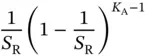
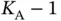 sensors chose it for transmission.
sensors chose it for transmission.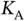 sensors is:
sensors is: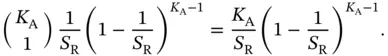
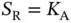 . Hence, the best way is to choose the number of reservation slots to be equal to the number of active sensors that are contending via random access (framed ALOHA), such that the probability of successful reception in a given slot is:
. Hence, the best way is to choose the number of reservation slots to be equal to the number of active sensors that are contending via random access (framed ALOHA), such that the probability of successful reception in a given slot is: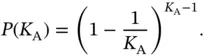
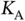 of active sensors in the total population of
of active sensors in the total population of 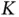 sensors.
sensors.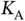 sensors that will be contending with each other in order to request access, but he does not know the identities of these sensors. Note that this is the crucial assumption in the problem setup for random access, since if Basil knows which
sensors that will be contending with each other in order to request access, but he does not know the identities of these sensors. Note that this is the crucial assumption in the problem setup for random access, since if Basil knows which 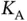 sensors will require access, then there is no need for randomized contention: namely, Basil can simply set
sensors will require access, then there is no need for randomized contention: namely, Basil can simply set 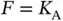 and allocate one data slot to each sensor. Although this observation seems trivial, it is very often overlooked when random access is considered in practical systems. Basil sets
and allocate one data slot to each sensor. Although this observation seems trivial, it is very often overlooked when random access is considered in practical systems. Basil sets 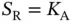 , but the number
, but the number 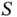 of sensors that successfully send reservation requests is random. This implies that the number of allocated slots
of sensors that successfully send reservation requests is random. This implies that the number of allocated slots 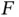 is also random. The expected value of
is also random. The expected value of 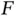 is
is 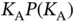 , and one can use (1.8)to calculate the expected goodput in a frame.
, and one can use (1.8)to calculate the expected goodput in a frame.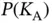 decreases with
decreases with 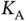 and it reaches
and it reaches 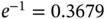 as the number of users goes to infinity. The engineering insight from
as the number of users goes to infinity. The engineering insight from 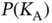 is that, when the users are contending in smaller groups, then the probability of successful transmission experienced by an individual user is higher.
is that, when the users are contending in smaller groups, then the probability of successful transmission experienced by an individual user is higher.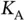 is rather artificial. On the other hand, Basil may know some statistics about the random process according to which the sensors send reservation requests. In that case, it can be reasonable to conclude that Basil knows the expected value of
is rather artificial. On the other hand, Basil may know some statistics about the random process according to which the sensors send reservation requests. In that case, it can be reasonable to conclude that Basil knows the expected value of 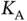 . Although not mathematically rigorous, Basil can work with the expected value as if it is the exact value and use the following approach. At the start of
. Although not mathematically rigorous, Basil can work with the expected value as if it is the exact value and use the following approach. At the start of 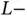 th frame the expected number of sensors that require access, denoted by
th frame the expected number of sensors that require access, denoted by 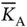 , is given by:
, is given by: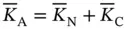
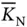 is the expected number of new requests generated from new sensors in the previous,
is the expected number of new requests generated from new sensors in the previous,  th frame.
th frame. 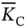 is the expected number of sensors that tried to send request in the previous frames, but did not succeed due to collision. If a frame becomes sufficiently long, then we can apply the law of large numbers, by which the expected values can be approximated as the exact values. For this to be true, the random arrival process of the requests from the sensors should satisfy certain conditions, which we will not discuss in detail here. It suffices to say that, for example, Poisson arrivals of requests over a sufficiently long interval would work. Going back to (2.4), we remove the averaging bar and recast the same equation as
is the expected number of sensors that tried to send request in the previous frames, but did not succeed due to collision. If a frame becomes sufficiently long, then we can apply the law of large numbers, by which the expected values can be approximated as the exact values. For this to be true, the random arrival process of the requests from the sensors should satisfy certain conditions, which we will not discuss in detail here. It suffices to say that, for example, Poisson arrivals of requests over a sufficiently long interval would work. Going back to (2.4), we remove the averaging bar and recast the same equation as 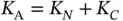 . Using the previous analysis on the probability of successful transmission of a request, we can express
. Using the previous analysis on the probability of successful transmission of a request, we can express 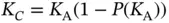 , but since
, but since 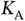 is large, we can write
is large, we can write 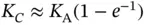 , which leads to:
, which leads to:










