12 Chapter 12Figure 12.1 The sphere as a two-dimensional manifold in 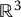 .Figure 12.2 Integral manifold in
.Figure 12.2 Integral manifold in 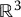 .Figure 12.3 Pictorial representation of a vector field on a manifold.Figure 12.4 Inner-loop/outer-loop control architecture for feedback linearization.Figure 12.5 Single-link, flexible joint robot.Figure 12.6 Step response and motor torque of the flexible joint robot. The difference betw...Figure 12.7 Tracking response and motor torque of the flexible joint robot with a cubic pol...Figure 12.8 Tracking response and motor torque of the flexible joint robot with an observer...
.Figure 12.3 Pictorial representation of a vector field on a manifold.Figure 12.4 Inner-loop/outer-loop control architecture for feedback linearization.Figure 12.5 Single-link, flexible joint robot.Figure 12.6 Step response and motor torque of the flexible joint robot. The difference betw...Figure 12.7 Tracking response and motor torque of the flexible joint robot with a cubic pol...Figure 12.8 Tracking response and motor torque of the flexible joint robot with an observer...
13 Chapter 13Figure 13.1 An underactuated serial-link robot.Figure 13.2 Upper-actuated (left) and lower-actuated (right) robots.Figure 13.3 Illustrating common reference angle conventions.Figure 13.4 The inverted pendulum on a cart.Figure 13.5 An overhead crane, a gimballed rocket and bipedal walking as examples of the in...Figure 13.6 The Acrobot as a gymnastic robot.Figure 13.7 The Pendubot.Figure 13.8 The Reaction-Wheel Pendulum.Figure 13.9 The Reaction Wheel Pendulum.Figure 13.10 Equilibrium configurations of the Acrobot and Pendubot under gravity with zero ...Figure 13.11 Local stabilization of the Reaction-Wheel Pendulum at the inverted position q ...Figure 13.12 Equilibrium configurations of the Pendubot for ue nonzero.Figure 13.13 The determinant of the controllability matrix for equilibrium positions (0, π/2...Figure 13.14 Brachiation motion of the Acrobot with virtual holonomic constraint q 1+ 0....Figure 13.15 A simple pendulum with a force F acting at the bob.Figure 13.16 Phase portrait of the simple pendulum. The constant energy curves are solution ...Figure 13.17 Phase portrait of the closed-loop system. Figure generated by pplane, courtesy ...Figure 13.18 The Reaction-Wheel Pendulum as a parallel interconnection of passive systems.Figure 13.19 Swingup and balance of the Reaction-Wheel Pendulum (left) and phase plane traje...Figure 13.20 Reaction-wheel velocity (left) and saturated control input (right).Figure 13.21 Swingup and balance of the Acrobot using switching control
14 Chapter 14Figure 14.1 Mass m connected to a rigid rod.Figure 14.2 The rolling disk.Figure 14.3 The kinematic car.Figure 14.4 A hopping robot.Figure 14.5 The differential drive robot: top view (left), side view (right).Figure 14.6 The car parking problem.Figure 14.7 Illustrating the notion of Lie bracket direction.Figure 14.8 Response of z 1, z 2, and z 3: Note that z 1and z 2return to t...Figure 14.9 Response of z 1, z 2and z 3.Figure 14.10 Trajectory and control inputs of the DDR computed from the flat outputs.Figure 14.11 Sliding-mode control of the DDR in chain form: response of the chain variables ...Figure 14.12 Sliding-mode control of the DDR in chain form: control inputs.Figure 14.13 Modified sliding-mode control of the DDR in chain form: response of the chain v...Figure 14.14 Modified sliding-mode control of the DDR in chain form: control inputs.Figure 14.15 DDR pose regulation.Figure 14.16 Differential drive robot showing the location of the output located d units a...Figure 14.17 Trajectory of the differential drive robot with partial feedback linearization ...
15 Appendix BFigure 1: The right hand rule.
16 Appendix CFigure C.1: Illustrating the definition of stability.
1 Cover
2 Table of Contents
3 Preface
1 iii
2 iv
3 v
4 vi
5 vii
6 viii
7 ix
8 1
9 2
10 3
11 4
12 5
13 6
14 7
15 8
16 9
17 10
18 11
19 12
20 13
21 14
22 15
23 16
24 17
25 18
26 19
27 20
28 21
29 22
30 23
31 24
32 25
33 26
34 27
35 28
36 29
37 30
38 31
39 32
40 33
41 35
42 36
43 37
44 38
45 39
46 40
47 41
48 42
49 43
50 44
51 45
52 46
53 47
54 48
55 49
56 50
57 51
58 52
59 53
60 54
61 55
62 56
63 57
64 58
65 59
66 60
67 61
68 62
69 63
70 64
71 65
72 66
73 67
74 68
75 69
76 70
77 71
78 72
79 73
80 74
81 75
82 76
83 77
84 78
85 79
86 80
87 81
88 82
89 83
90 84
91 85
92 86
93 87
94 88
95 89
96 90
97 91
98 92
99 93
100 94
101 95
102 96
103 97
104 98
105 99
106 100
107 101
108 102
109 103
110 104
111 105
112 106
113 107
114 108
115 109
116 110
117 111
118 112
119 113
120 114
121 115
122 116
123 117
124 118
125 119
126 120
127 121
128 122
129 123
130 124
131 125
132 126
133 127
134 128
135 129
136 130
137 131
138 132
139 133
140 134
141 135
142 136
143 137
144 138
145 139
146 140
147 141
148 142
149 143
150 144
151 145
152 146
153 147
154 148
155 149
156 150
157 151
158 152
159 153
160 154
161 155
162 156
163 157
164 158
165 159
166 160
167 161
168 162
169 163
170 165
171 166
172 167
173 168
174 169
175 170
176 171
177 172
178 173
179 174
180 175
181 176
182 177
183 178
184 179
185 180
186 181
187 182
188 183
189 184
190 185
191 186
192 187
193 188
194 189
195 190
196 191
197 192
198 193
199 194
200 195
201 196
202 197
203 198
204 199
205 200
206 201
207 202
208 203
209 204
210 205
211 206
212 207
213 208
214 209
215 210
216 211
217 212
218 213
219 214
220 215
221 216
222 217
223 218
224 219
225 220
226 221
227 222
228 223
229 224
230 225
231 226
232 227
233 228
234 229
235 230
236 231
237 232
238 233
239 234
240 235
241 236
242 237
243 238
244 239
245 240
246 241
247 242
248 243
249 244
250 245
251 246
252 247
253 248
254 249
255 250
256 251
257 252
258 253
259 254
260 255
261 256
262 257
263 258
264 259
265 260
266 261
267 262
268 263
269 264
270 265
271 266
272 267
273 268
274 269
275 271
276 272
277 273
278 274
279 275
280 276
281 277
282 278
283 279
284 280
285 281
286 282
287 283
288 284
289 285
290 286
291 287
292 288
293 289
294 290
295 291
296 292
297 293
298 294
299 295
300 296
301 297
302 298
303 299
304 300
305 301
306 302
307 303
308 304
309 305
310 306
311 307
312 308
Читать дальше

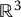 .Figure 12.2 Integral manifold in
.Figure 12.2 Integral manifold in 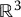 .Figure 12.3 Pictorial representation of a vector field on a manifold.Figure 12.4 Inner-loop/outer-loop control architecture for feedback linearization.Figure 12.5 Single-link, flexible joint robot.Figure 12.6 Step response and motor torque of the flexible joint robot. The difference betw...Figure 12.7 Tracking response and motor torque of the flexible joint robot with a cubic pol...Figure 12.8 Tracking response and motor torque of the flexible joint robot with an observer...
.Figure 12.3 Pictorial representation of a vector field on a manifold.Figure 12.4 Inner-loop/outer-loop control architecture for feedback linearization.Figure 12.5 Single-link, flexible joint robot.Figure 12.6 Step response and motor torque of the flexible joint robot. The difference betw...Figure 12.7 Tracking response and motor torque of the flexible joint robot with a cubic pol...Figure 12.8 Tracking response and motor torque of the flexible joint robot with an observer...










