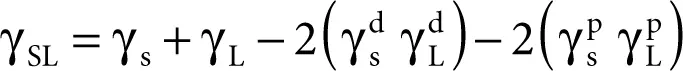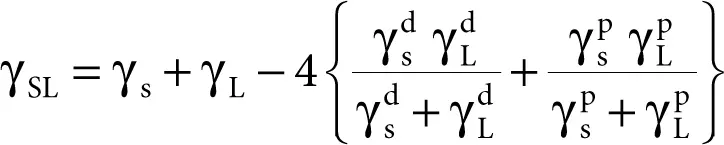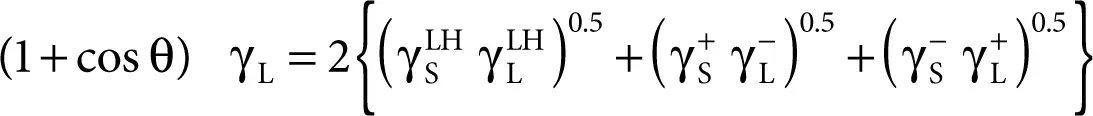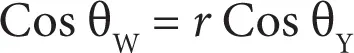(2.7)
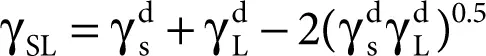
Fowkes [25] modified Equation 2.7 by changing from geometric mean to arithmetic mean to arrive at the following equation:
(2.8)
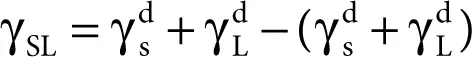
Owens and Wendt [26] significantly changed the Fowkes idea while assuming that the sum of all the components occurring on the right-hand side of Equation 2.11, namely
except that γ dcan be considered as associated with the polar interaction  ,
,
Consequently, the following equation was obtained:
(2.9)
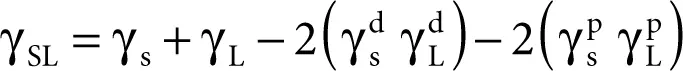
Wu [27, 28] accepted the idea by Owens and Wendt to divide the SFE into two parts, but used the harmonic means of the interfacial interactions instead of the geometric means in Equation 2.9 and derived the following equation:
(2.10)
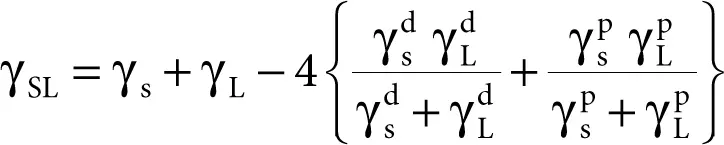
van Oss, Chaudhury, and Good proposed the latest concept of partition in which surface energy is partitioned into two components [29, 30]:
1 Long range interactions London, Keesom, and Debye called the Lifshitz–van der Waals component (γLW)
2 The short-range interactions (acid–base), called the acid–base component (γAB) = 2(γ+ γ–)0.5 where γ+ and γ– mean the acidic and basic constituents, respectively, which are associated with the acid–base interactions.
Combining van Oss Chaudhury’s concept with Young’s equation (Equation 2.5), we obtain the Young–Fowkes–van Oss–Good acid–base equation referred to as the acid–base approach:
(2.11)
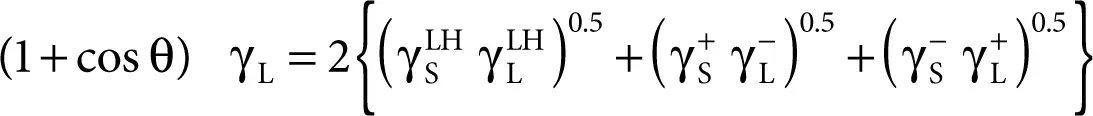
This equation contains three unknowns and, therefore, we need contact angle data of three liquids. Table 2.3contains the physical properties and surface free energy components of test liquids normally used. One of them must be non-polar and the other two should be polar. The Lifshitz–van der Waals component of the surface free energy is obtained from the contact angle of the apolar test liquid, e.g., diiodomethane.
Table 2.3 Physical properties and surface free energy components of test liquids used at 20°C [31].
| Liquid |
Density (kg/m3) |
Viscosity (mPas) |
Surface free energy (mJm–2) (LW–AB approach) |
|
|
|
|
γlv |
| Water |
1000 |
1.00 |
21.8 |
25.5 |
25.5 |
51.0 |
72.8 |
| Formamide |
799 |
1.02 |
39 |
2.28 |
39.6 |
19 |
58 |
| Ethylene glycol |
1109 |
19.9 |
29 |
1.92 |
47 |
19 |
48 |
| Diethylene glycol |
1130 |
26.8 |
44.7 |
– |
– |
– |
– |
| Diodomethane |
3325 |
2.8 |
50.8 |
0 |
0 |
0 |
50.8 |
| 1-Bromonaphthalene |
1483 |
– |
44.4 |
0 |
0 |
0 |
44.4 |
The acid–base interaction and its relevance to adhesives and adhesive bonding have been reviewed in detail by Chehimi et al. [32].
2.12 Spreading Coefficient
For spreading, another parameter, the spreading coefficient γ SV– γ SL– γ LVappears to be important in classifying liquids that have a tendency to form good films on a given substrate. In general, the larger and more positive value of the spreading coefficient (S), the more energy is gained by intercalating a liquid film between a solid and air. Thus,
S > 0, spontaneous spreading
S > 0, not spontaneous spreading
Though the condition S > 0 is necessary for a liquid to spread spontaneously on a solid, it is insufficient to describe the final state of the film.
2.13 Zisman’s Rectilinear Relationship—Zisman’s Plots and Critical Surface Tension of a Solid
Fox and Zisman [33] introduced the well-known concept of critical surface tension, γ c. In the method adopted by Zisman, the contact angles θ for a series of organic homologous liquids were measured on a solid. A plot of cos θ vs. surface tension of the liquids gave a straight line ( Figure 2.6). The point of intersection of the straight line and the line through cos θ = 1 is the “critical surface tension” γ cof the solid. All liquids whose surface tension is less than the critical surface tension will wet the substrate.
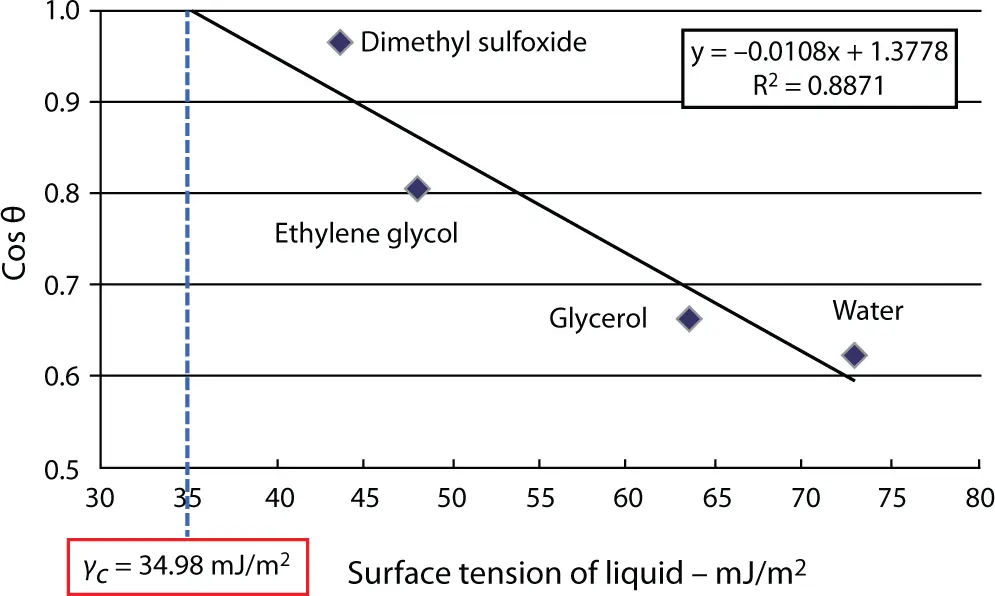
Figure 2.6 Zisman’s plot ( https://www.researchgate.net/publication/279532584_Analysis_of_the_Results_of_Surface_Free_Energy_Measurement_of_Ti6Al4V_by_Different_Methods/figures?lo=1).
2.14 Effect of Surface Roughness on Contact Angle
The above equation is true for smooth, contamination-free surface. However, the real solid surface is not smooth and the roughness of the surface has a profound effect on the wetting and adhesion. The innumerable small hills, valleys, and crevices on the solid surface entrap and occlude air or vapor within them. Even if θ = 0, it is not possible under real conditions to ensure that an intimate contact between the adhesive and adherend is established. Surface roughness plays therefore an important role in the wettability of a solid surface.
The impact of roughness on the contact angle is given by the Wenzel equation (Equation 2.12)
(2.12)
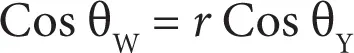
The Wenzel equation (Equation 2.12) relates the contact angle θw of a liquid measured on a rough surface having a roughness ratio, r , with the contact angle of the same liquid measured on a smooth surface, θ Y. The roughness ratio is the ratio of the true surface area of a rough surface to the surface area of the smooth surface. This ratio r will always be larger than one. Wenzel’s relation also shows that surface roughness will decrease the contact angle for a water droplet on a hydrophilic surface or increase the contact angle for a water droplet on a hydrophobic surface.
The advancing and receding contact angles can throw light on the magnitude of roughness of the wood surface. The difference between advancing and receding contact angles is the contact angle hysteresis. The magnitude of contact angle hysteresis is dependent on roughness, topography, morphology, and chemical homogeneity of the solid surface [31]. Good [34] suggested that the advancing contact angle represents hydrophobic areas on the surface, while the receding contact angle characterizes hydrophilic areas.
Читать дальше

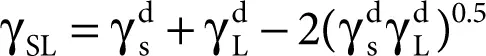
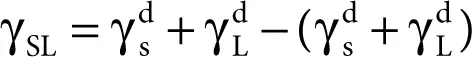
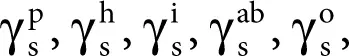
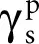 ,
,