R. N. Kumar - Adhesives for Wood and Lignocellulosic Materials

It is evident from the previous section that various interactions operate effectively only when the molecules of the adhesives come as close as possible to those of the substrate in order that such a proximity will lead to maximum mutual interaction. Such closeness is possible only when the adhesives wet the substrate.

Wetting is the ability of liquids to form interfaces with solid surfaces. To determine the degree of wetting, the contact angle (θ) that is formed between the liquid and the solid surface is measured. The smaller the contact angle and the smaller the surface tension, the greater the degree of wetting ( Figure 2.3).

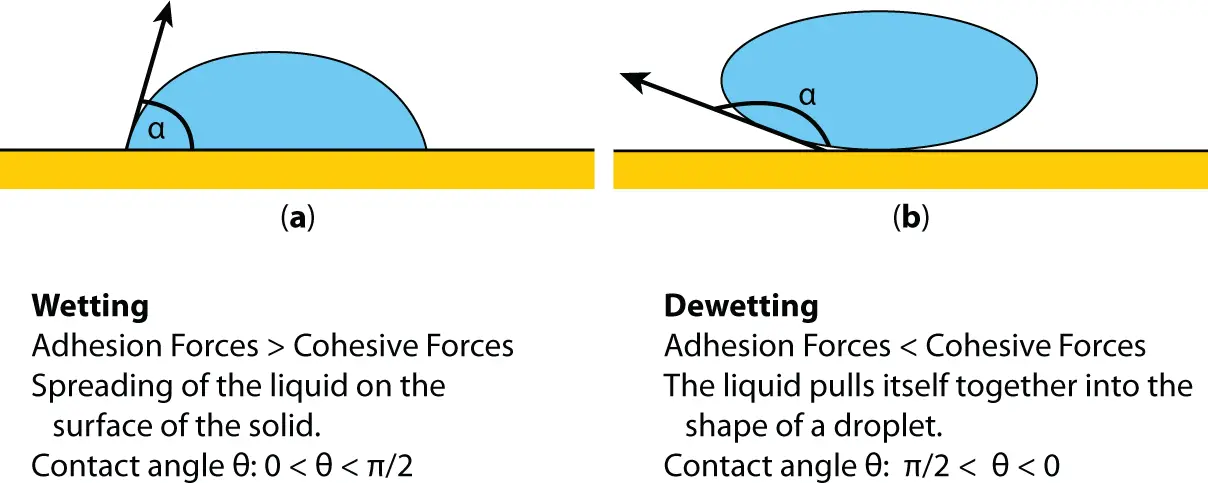
Figure 2.3 Wetting phenomenon.

For maximum adhesion, the adhesive must completely cover the substrate, i.e., spreading is necessary. The contact angle is a good indicator of adhesive behavior. This is illustrated in Figure 2.4.

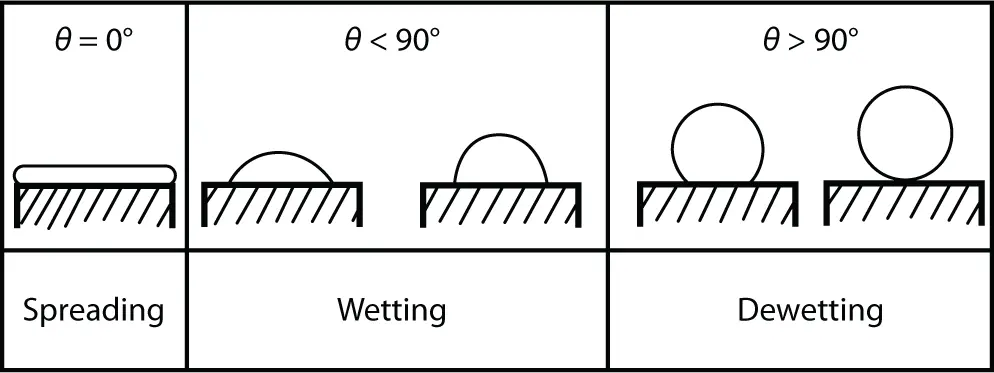
Figure 2.4 Wetting, spreading, and dewetting for different contact angles.

In 1805, Thomas Young provided the first good approach for describing wettability, spreading, and their relationship to the contact angle.

A drop of adhesive on a surface will come to equilibrium under the action of three forces as shown in Figure 2.5.

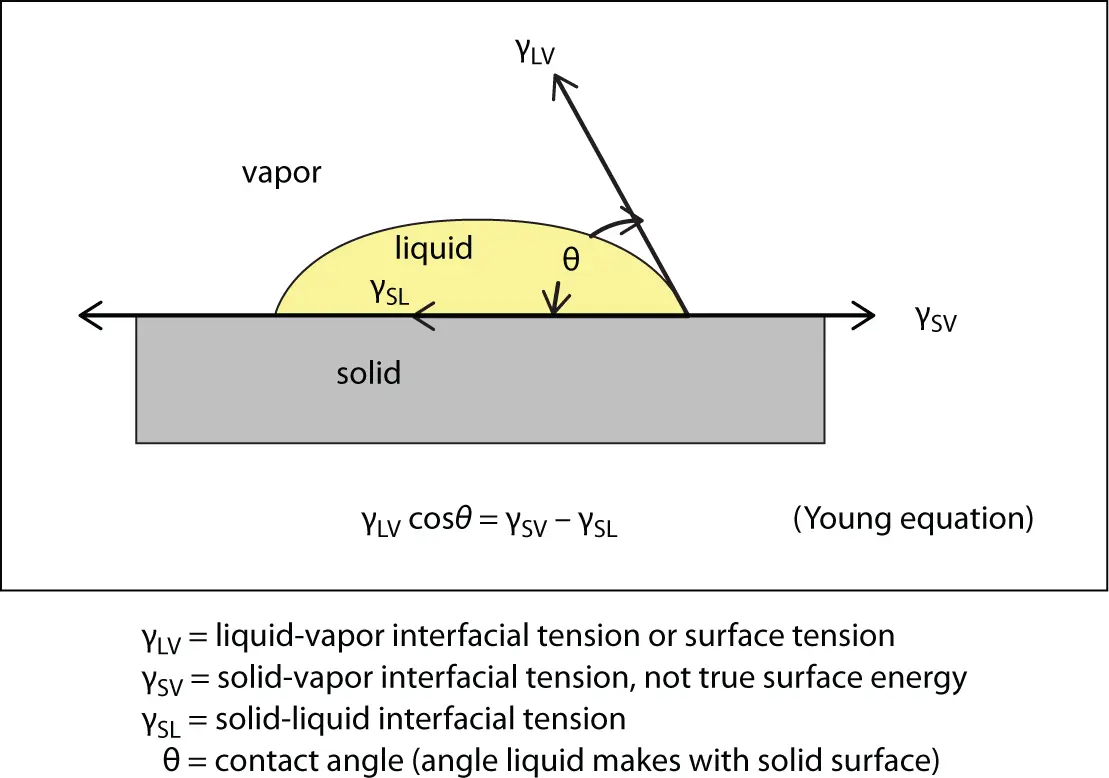
Figure 2.5 Equilibrium contact angle based on balance of forces.

Considering the component of γ LValong the X -axis, we can write the following force balance:

(2.1)

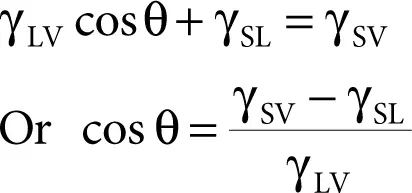
Thus, when θ = 0, the liquid spreads spontaneously on the substrate; in other words, when cos θ is high (i.e., as it approaches 1), there is spontaneous spreading.

From Equation 2.1, it is clear that wetting will be favored when the surface tension of the liquid is low.

Since the tendency of the liquid to wet and spread spontaneously increases as the contact angle decreases, the contact angle is a useful inverse measure of wetting or the cosine of the contact angle is a direct measure of wetting.

Perhaps the most convenient way of interpreting the wettability of a low energy solid is the formulation of the work of adhesion, W A, defined by Dupré and Dupré [22] as the work required to separate a unit area of the solid–liquid interface.

Consider the wetting of a solid substrate (S) by a liquid (adhesive) “L”. A solid–liquid interface is formed as a result according to the following equation:

(2.2)

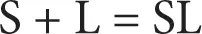
If γ S, γ L, and γ SLare the surface free energies of solid substrate, liquid (adhesive), and the interphase, then the free energy change of the process (Δ G A) can be written as

(2.3)

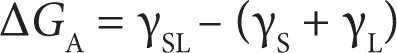
The work of adhesion W A= –Δ G can be written as

(2.4)

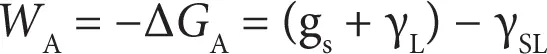
This is the thermodynamic work of adhesion or the work needed to separate unit area of the solid–liquid interface.

Assuming γ LV= γ Land γ SV= γ sfrom Equations 2.1 and 2.4, we get

(2.5)

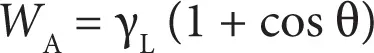
This is known as Young–Dupre’s equation. Thus, if the contact angle, θ, of a well-defined probe liquid against a solid is measured, the work of adhesion can be determined.

Thus, the thermodynamic work of adhesion (W) is, by definition, the free energy change per unit area required to separate to infinity two surfaces initially in contact with a result of creating two new surfaces at the interface between two materials, for example, an adhesive and an adherend.

It is related to the intermolecular forces that operate

at the interface between two materials, for example, an adhesive and an adherend.

It is related to the intermolecular forces that operate

at the interface between two materials, for example, an adhesive and an adherend.

It is related to the intermolecular forces that operate

at the interface between two materials, for example,

It is related to the intermolecular forces that operate

at the interface between two materials, for example,

Fowkes [23] proposed that both reversible work of adhesion (W) and the surface free energy (γ) had additive components and can be partitioned into individual components. Accordingly, several equations were proposed based on this important approach. This pioneering development of Professor Frederick M. Fowkes regarding the acid–base theory in adhesion have attracted the attention of several laboratories. A Festschrift in his honor on the occasion of his 75th birthday was published in 1991.

The approach is described below:

(1) Partitioning of surface free energies into components

The principle of partitioning is based on the assumption that the surface free energy is determined by various interfacial interactions. These interactions in turn depend on the basic properties of the interacting liquid and that of the solid–liquid interface (SL) [23, 24].

(2.6)

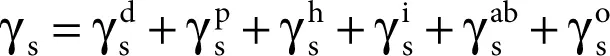
where =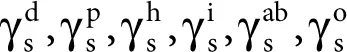

are the dispersion, polar, hydrogen (related to hydrogen bonds), induction, and acid–base components, respectively, while o refers to all remaining interactions.

(2) Mode of combinations of the individual energy components According to Fowkes, the dispersion component of the surface free energy is connected with the London interactions. The remaining van der Waals interactions, i.e., the Keesom and Debye ones, have been considered by Fowkes as a part of the induction interactions.

Fowkes investigated mainly two-phase systems containing a substance (solid or liquid) in which the dispersion interactions appear only. Considering just such systems, Fowkes determined the SFE corresponding to the solid–liquid interface as follows:

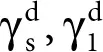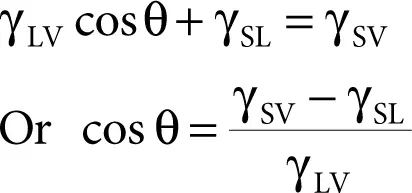
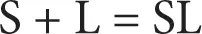
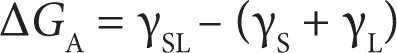
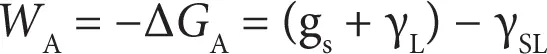
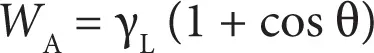
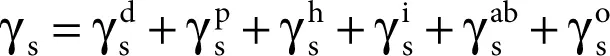
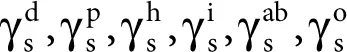
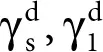For two-phase systems comprising of a solid and liquid, in which only dispersion interactions occur, namely, between , Fowkes employed geometric mean as the mode of combination of these energy components to give the following equation: