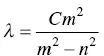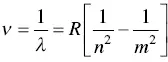George Domingo - Semiconductor Basics

Source: https://www.kruess.com/en/campus/spectroscopy/history‐of‐spectroscopy/.

Suppose you are roasting a chicken and carefully watching the dial of a digital thermometer inserted in the chicken's breast as the temperature increases from room temperature, 24 °C (degrees Celsius), to 80 °C, the recommended internal temperature of a well‐cooked chicken breast. As the temperature increases, suddenly the thermometer jumps from 39 °C to 41 °C, then from 56 °C to 58 °C, and finally from 66 °C to 68 °C. You wonder what is wrong with the thermometer: why don't the temperatures 40, 57, and 67 °C show up on the dial? They don't seem to exist. You buy a new thermometer, just to be sure, and find that exactly the same temperature values are missing. A third thermometer gives the same results. You place the same thermometers in soup, and the thermometers are well behaved, showing in succession the values 39, 40, and 41 °C. So, the thermometers work. The missing temperatures are no coincidence. There is something in that chicken that makes the temperature jump from one value to another without passing through the one in the middle.

Well, that was probably Wollaston's initial reaction. What separated the colors? Was the instrument lens dirty? He even considered the possibility that there were natural boundaries between certain colors. But why didn't these black boundaries appear when he pointed the spectrometer at a white light?

German physicist Joseph von Fraunhofer (1787–1826), on the right in Figure 1.2, studied these dark lines of the sun's spectrum in much more detail and actually named the missing lines with the letters A–K (not too imaginative; ancient astronomers would have found much more attention‐grabbing names).

The next step was to take a look at the emission of light from several metals, gases, and stars. The observers soon found that each element has its own unique set of lines. Take a look at Figure 1.4. White light through a prism generates a continuous spectrum (top diagram); no colors are missing. If we heat a gas until it glows and pass the light through the same prism (middle diagram), only certain lines are projected onto the screen: the rest of the spectrum has disappeared. But if we do it differently – that is, if we have the cold gas between the white light and the prism (bottom diagram) – then the full spectrum appears, except for exactly the same lines that were visible in the previous spectral measurement. The superposition of the middle and lower spectra is equal to the spectrum of the white light at the top. The gas, when cold, absorbs the same specific light waves as the ones it emits when it glows. What a coincidence! And this happens with all gases and materials. The lines are at different frequencies, but all of them have lines.

Figure 1.4 The spectrum from any gas shows similar but different missing lines (middle image), but when the same gas is hot and emits light, only the lines that were black before are now visible (lower image).

Source: https://quizlet.com/102018176/astronomy‐4‐spectroscopy‐flash‐cards/.

In 1766, an English aristocrat named Henry Cavendish (1731–1810) was the first to recognize hydrogen as an element, that is, a unique substance and an integral part of the water molecule. By the time Dmitri Mendeleev (1834–1907) published his now ubiquitous periodic table of the elements in 1869, 100 years later, it was already known that hydrogen was the lightest of all the known elements (at that time, 60 elements were known). Mendeleev ( Figure 1.5) reordered the known elements by their relative atomic weight, with hydrogen as 1.

Figure 1.5 Dmitri Mendeleev and the periodic table with the elements known in his time and the empty slots for elements still to be discovered.

Source: Wikipedia, https://en.wikipedia.org/wiki/Dmitri_Mendeleev#/media/File:Dmitri_Mendeleev_1890s.jpg.

Johann Balmer (1825–1898), a Swiss mathematician, found empirically in 1895 that the separation of the optical lines generated by hydrogen gas can be expressed by a formula using just a constant, C , and integer numbers. He expressed his observation with Eq. (1.3)

(1.3)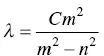

here λ is the wavelength of the missing line, C is a heuristically obtained constant ( C = 3.64 × 10 −9m), n = 2, and m is an integer greater than 2 (i.e. 3, 4, 5, and so on). When you put any of these integer numbers in Eq. (1.3), you get the wavelength of all the lines in the hydrogen spectrum.

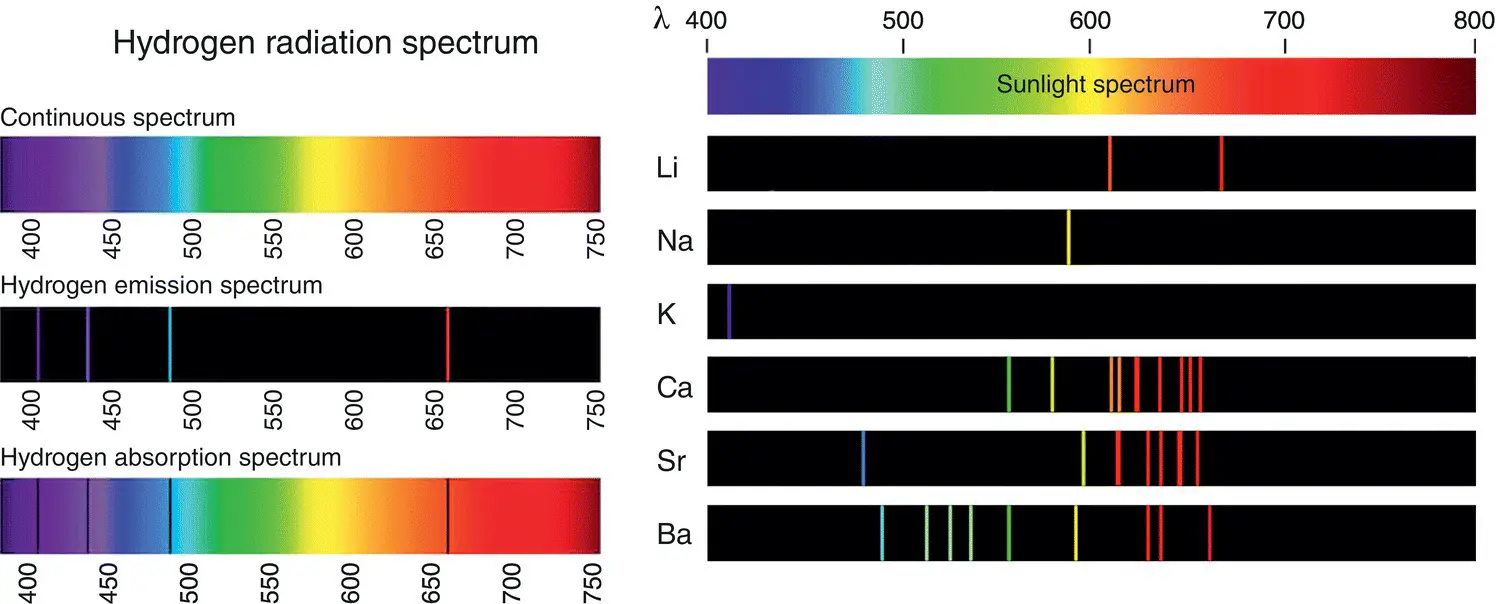
Figure 1.6 The spectrum of the hydrogen atom on the left shows the absorption lines (below) and the emission lines (middle). On the right are the emission lines of several other materials.

Source: https://www.shutterstock.com/image‐vector/spectrum‐spectral‐line‐example‐hydrogen‐emission‐1288942888?src=iUiOwiDEznOcV6XzswXhMA‐1‐0(left); https://www.shutterstock.com/image‐vector/line‐spectra‐elements‐339037577?src=I6tWF1qlh6XcWayXsZl‐Gw‐3‐16(right).

Figure 1.6shows the hydrogen spectrum on the left, with its characteristic emission and absorption lines. These are the lines that Balmer used to develop Eq. (1.3)to calculate the missing hydrogen's wavelengths. All the elements have similar absorption and emission lines at different wavelengths, and I show a few on the right in Figure 1.6.

Just three years later, Johannes Rydberg (1854–1919) found that the Balmer equation was one specific case of a more general formula, Eq. (1.4):

(1.4)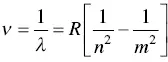

The reciprocal of the wavelength is now given by a constant R and the same integer numbers, except that now n is allowed to have different integer numbers: 2, 3, 4, and so on. R is also a heuristically derived constant ( R = 1.1 × 10 7m −1), called the Rydberg constant . Both Balmer and Rydberg ( Figure 1.7) were able to quantify the entire spectrum of the hydrogen atom using the relationship in Eq. (1.4). It is interesting that Niels Bohr, whom I'll talk more about in Section 1.8, was able to calculate the Rydberg number using fundamental physical values, such as the mass of the electron, the electronic charge, the permittivity of free space, Planck's constant, and the speed of light (see Appendix 1.3). This behavior screams for an explanation.

Figure 1.7 Johann Balmer (left) found a mathematical relation for hydrogen's spectral lines, and Johannes Rydberg (right) came up with a more general equation applicable to all gases and materials.