Ned Mohan - Analysis and Control of Electric Drives

In many high‐performance systems, drives are required to operate in all four quadrants of the torque‐speed plane, as shown in Fig. 2-16b.

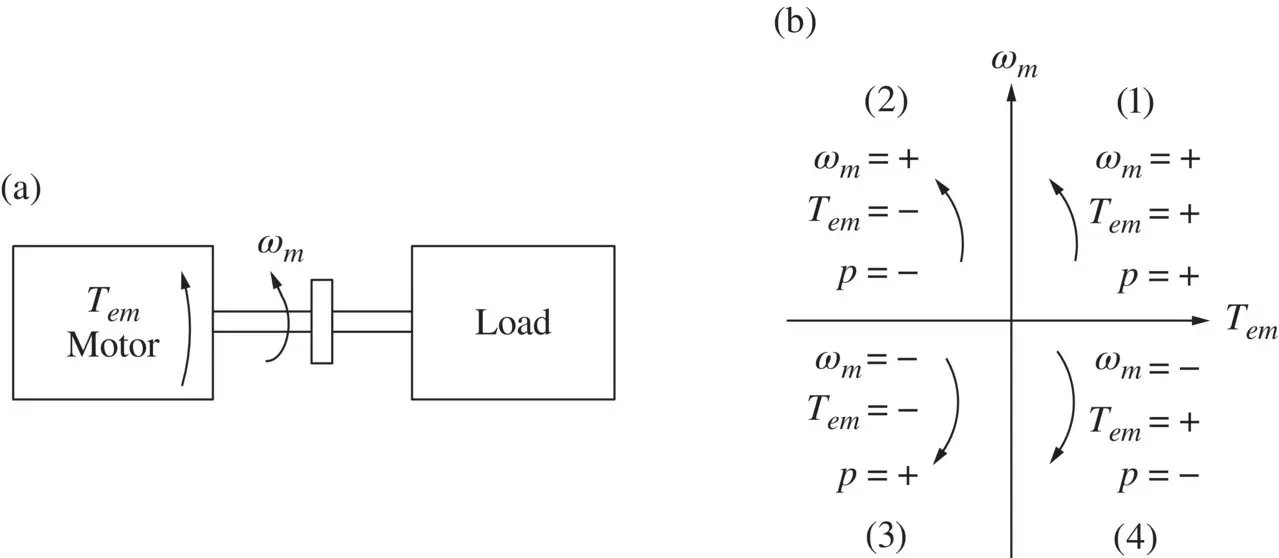
Fig. 2-16 (a) Electric drive and (d) four-quadrant operation.

The motor drives the load in the forward direction in quadrant 1, and in the reverse direction in quadrant 3. In both of these quadrants, the average power is positive and flows from the motor to the mechanical load. In order to control the load speed rapidly, it may be necessary to operate the system in the regenerative braking mode, where the direction of power is reversed, so that it flows from the load into the motor, and usually into the utility (through the power‐processing unit). In quadrant 2, the speed is positive, but the torque produced by the motor is negative. In quadrant 4, the speed is negative and the motor torque is positive.

As discussed in Section 2‐8, each load has its own torque‐speed characteristic. For high‐performance drives, in addition to the steady‐state operation, the dynamic operation – how the operating point changes with time – is also important. The change of speed of the motor‐load combination should be accomplished rapidly and without any oscillations (which otherwise may destroy the load). This requires a good design of the closed‐loop controller, as discussed in Chapter 5, which deals with the control of drives.

1 1. What are the MKS units for force, torque, linear speed, angular speed, speed, and power?

2 2. What is the relationship between force, torque, and power?

3 3. Show that torque is the fundamental variable in controlling speed and position.

4 4. What is the kinetic energy stored in a moving mass and a rotating mass?

5 5. What is the mechanism for torsional resonances?

6 6. What are the various types of coupling mechanisms?

7 7. What is the optimum gear ratio to minimize the torque required from the motor for a given load‐speed profile as a function of time?

8 8. What are the torque‐speed and the power‐speed profiles for various types of loads?

1 1. Bosch (1993). Automotive Handbook. Robert Bosch GmbH.

2 2. Nondahl, T. (1998). Proceedings of the NSF/EPRI‐Sponsored Faculty Workshop on “Teaching of Power Electronics” (25–28 June 1998). University of Minnesota.

1 Gross, H. (ed.) (1983). Electric Feed Drives for Machine Tools. New York: Siemens and Wiley.

2 (1980). DC Motors and Control ServoSystem – An Engineering Handbook, 5e. Hopkins, MN: Electro‐Craft Corporation.

3 Spong, M. and Vidyasagar, M. (1989). Robot Dynamics and Control. Wiley.

1 2‐1 A constant torque of 5 Nm is applied to an unloaded motor at rest at time t = 0. The motor reaches a speed of 1800 rpm in 3 s. Assuming the damping to be negligible, calculate the motor inertia.

2 2‐2 Calculate the inertia if the cylinder in Example 2-2is hollow, with the inner radius r2 = 4 cm.

3 2‐3 A vehicle of mass 1500 kg is traveling at a speed of 50 km/h. What is the kinetic energy stored in its mass? Calculate the energy that can be recovered by slowing the vehicle to a speed of 10 km/h.

1 2‐4 Consider the belt and pulley system in Fig. 2-13. Inertias other than that shown in the figure are negligible. The pulley radius r = 0.09 m and the motor inertia JM = 0.01 kg ⋅ m2. Calculate the torque Tem required to accelerate a load of 1.0 kg from rest to a speed of 1 m/s in a time of 4s. Assume the motor torque to be constant during this interval.

2 2‐5 For the belt and pulley system shown in Fig. 2-13, M = 0.02 kg. For a motor with inertia JM = 40 g ⋅ cm2, determine the pulley radius that minimizes the torque required from the motor for a given load‐speed profile. Ignore damping and the load force fL.

1 2‐6 In the gear system shown in Fig. 2-14, the gear ratio nL/nM = 3 where n equals the number of teeth in gear. The load and motor inertia are JL = 10 kg ⋅ m2 and JM = 1.2 kg ⋅ m2. Damping and the load‐torque TL can be neglected. For the load‐speed profile shown in Fig. 2-1b, draw the profile of the electromagnetic torque Tem required from the motor as a function of time.

2 2‐7 In the system of Problem 2-6, assume a triangular speed profile of the load with equal acceleration and deceleration rates (starting and ending at zero speed). Assuming a coupling efficiency of 100%, calculate the time needed to rotate the load by an angle of 30o if the magnitude of the electromagnetic torque (positive or negative) from the motor is 500 Nm.

3 2‐8 The vehicle in 2-8Exampleis powered by motors that have a maximum speed of 5000 rpm. Each motor is coupled to the wheel using a gear mechanism. (a) Calculate the required gear ratio if the vehicle’s maximum speed is 150 km/h, and (b) calculate the torque required from each motor at the maximum speed.

4 2‐9 Consider the system shown in Fig. 2-14. For JM = 40 g ⋅ cm2 and JL = 60 g ⋅ cm2, what is the optimum gear ratio to minimize the torque required from the motor for a given load‐speed profile? Neglect damping and external load torque.

1 2‐10 Consider the lead‐screw drive shown in Fig. P2-10. Derive the following equation in terms of pitch s, where = linear acceleration of the load, JM = motor inertia, Js = screw arrangement inertia, and the coupling ratio : Fig. P2-10 Lead‐screw system.

1 2‐11 In wind turbines, the shaft power available is given as follows, where the pitch‐angle θ is nearly zero to “catch” all the wind energy available: where Cp is the wind‐turbine Coefficient of Performance (a unit‐less quantity), ρ is the air density, Ar is the area swept by the rotor‐blades, and VW is the wind speed, all in MKS units. The rotational speed of the wind turbine is controlled, such that it is operating near its optimum value of the coefficient of performance with Cp = 0.48. Assume the combined efficiency of the gear‐box, the generator, and the power electronic converter to be 90%, and the air density to be 1.2 kg/m3, Ar = 4000 m2. Calculate the electrical power output of such a wind turbine at its rated wind speed of 13 m/s.

2 2‐12 A wind turbine is rotating at 22 rpm in steady state at a wind speed of 13 m/s and producing 1.5 MW of power. The inertia of the mechanism is 3.4 × 106kg ⋅ m2. Suddenly, there is a short‐circuit on the electric grid and the electrical output goes to zero for two seconds. Calculate the increase in speed in rpm during this interval. Assume that the shaft‐torque remains constant and all other efficiencies to be 100% for the purpose of this calculation.

3 2‐13 In an electric vehicle, each wheel is powered by its own motor. The vehicle weight is 2000 kg. This vehicle increases in its speed linearly from 0 to 60 mph in 10 seconds. The tire diameter is 70 cm. Calculate the maximum power required from each motor in kW.

4 2‐14 In an electric vehicle, each of the four wheels is supplied by its own motor. This EV weighs 1000 kg, and the tire diameter is 50 cm. Using regenerative braking, its speed is brought from 20 m/s (72 km/h) to zero in 10 seconds, linearly with time. Neglect all losses. Calculate and plot, as a function of time for each wheel, the following: (a) the electromagnetic deceleration torque Tem in Nm, (b) rotation speed ωm in rad/s, and (c) power Pm recovered in kW. Label the plots.