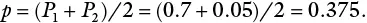Given a recombination value of r between two linked genes, the segregation in the second generation depends on the initial cross, as M.D. Haywood and E.L. Breese demonstrated as follows:
| Initial cross |
Free |
Homozygous potential |
| 1. AABB × aabb |
1(1 − r ) |
2 r |
| 2. AAbb × aaBB |
2 r |
2( r − 1) |
The second cross shows genes linked in the repulsion phase. The flow of variability from the homozygous potential to the free state depends on how tight a linkage exists between the genes. It will be at its maximum when r = 0.5 and recombination is free, and diminish with diminishing r . This illustration shows that with more than two closely linked loci on the same chromosome, the flow of variability would be greatly restricted. In species where selfing is the norm (or when a breeder enforces complete inbreeding), the proportion of heterozygotes will be reduced by 50% in each generation, dwindling to near zero by the 8th or 9th generation.
The open system of pollination in cross‐pollinated species allows each plant in the gene pool to have both homozygous and heterozygous loci. Plant breeders exploit this heterozygous genetic structure of individuals in population improvement programs. In a natural environment, the four factors of genetic change mentioned previously are operational. Fitness or adaptive genes will be favored over nonadaptive ones. Plant breeders impose additional selection pressure to hasten the shift in the population genetic structure toward adaptiveness as well as increase the frequencies of other desirable genes.
An example of a breeding application of Hardy‐Weinberg equilibrium
In disease resistance breeding, plant breeders cross an elite susceptible cultivar with one that has disease resistance. Consider a cross between two populations, susceptible × resistant. If the gene frequencies of an allele A in the two populations are represented by P 1and P 2, the gene frequency in the F 1 = (P 1 + P 2 )/2 = p . Assuming the frequency of the resistance gene in the resistant cultivar is P 1= 0.7 and that in the susceptible elite cultivar is P 2= 0.05, the gene frequency in the progeny of the cross p would be obtained as follows;
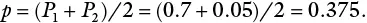
Consequently, the gene frequency for the resistant trait is reduced by about 50% (from 0.7 to 0.375).
3.2 Issues arising from Hardy‐Weinberg equilibrium
In order for Hardy‐Weinberg equilibrium to be true, several conditions must be met. However, some situations provide approximate conditions to satisfy the requirements.
3.2.1 Issue of population size
The Hardy‐Weinberg equilibrium requires a large random mating population (among other factors as previously indicated) to be true. However, in practice, the law has been found to be approximately true for most of the genes in most cross‐pollinated species, except when non‐random mating (e.g. inbreeding and assortative mating – discussed next) occur. Whereas inbreeding is a natural feature of self‐pollinated species, assortative mating can occur when cross‐pollinated species are closely spaced in the field.
3.2.2 Issue of multiple loci
Research has shown that it is possible for alleles at two loci to be in random mating frequencies and yet not in equilibrium with respect to each other. Further, equilibrium between two loci is not attained after one generation of random mating as Hardy‐Weinberg law concluded, but is attained slowly over many generations. Also, the presence of genetic linkage will further slow the rate of attainment of equilibrium ( Figure 3.2). If there is no linkage ( c = 0.5), the differential between actual frequency and the equilibrium frequency is reduced by 50% in each generation. At this rate, it would take about seven generations to reach approximate equilibrium. However, at c = 0.01 and c = 0.001, it would take about 69 and 693 generations, respectively, to reach equilibrium. A composite gene frequency can be calculated for genes at the two loci. For example, if the frequency at locus Aa = 0.2 and that for locus bb = 0.7, the composite frequency of a genotype Aabb = 0.2 × 0.7 = 0.14.
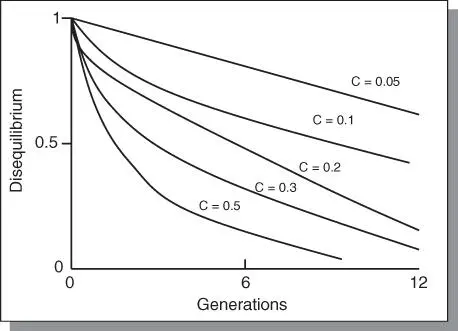
Figure 3.2The approach to linkage equilibrium under random mating of two loci considered together. The value of “c” gives the linkage frequency between two loci. The effect of linkage is to slow down the rate of approach, the closer the linkage, the slower the rate. For c = 5, there is no linkage. The equilibrium value is approached slowly and theoretically unattainable.
3.3 Factors affecting changes in gene frequency
Gene frequency in a population may be changed by one of two primary types of processes: systematicor dispersive. A systematic process causes a change in gene frequency that is predictable in both direction and amount. A dispersive process, associated with small populations, is predictable only in amount, not direction. D.S. Falconer listed the systematic processes as migration, mutation,and selection.
Migration is important in small populations. It entails the entry of individuals into an existing population from outside. Because plants are sedentary, migration, when it occurs naturally, is via pollen transfer (gamete migration). The impact of this immigration will have on the recipient population will depend on the immigration rate and the difference in gene frequency between the immigrants and natives. Mathematically, ∆ q = m ( q m− q o), where ∆ q = the changes in the frequency of genes in the new mixed population, m = the number of immigrants, q m= the gene frequency of the immigrants, and q o= gene frequency of the host. Plant breeders employ this process to change frequencies when they undertake introgression of genes into their breeding populations. The breeding implication is that for open‐pollinated (outbreeding) species, the frequency of the immigrant gene may be low, but its effect on the host gene and genotypes could be significant.
Natural mutations are generally rare. A unique mutation (non‐recurrent mutation) would have little impact on gene frequencies. Mutations are generally recessive in gene action, but the dominant condition may also be observed. Recurrent mutation (occurs repeatedly at a constant frequency) may impact gene frequency of the population. Natural mutations are of little importance to practical plant breeding. However, breeders may artificially induce mutation to generate new variability for plant breeding.
Selection is the most important process for altering population gene frequencies by plant breeders. Its effect is to change the mean value of the progeny population from that of the parental population. This change may be greater or lesser than the population mean, depending on the trait of interest. For example, breeders aim for higher yield but may accept and select for less of a chemical factor in the plant that may be toxic in addition to the high yield. For selection to succeed there must be:
Читать дальше