Many block ciphers use a more complex structure, which was invented by Feistel and his team while they were developing the Mark XII IFF in the late 1950s and early 1960s. Feistel then moved to IBM and founded a research group that produced the Data Encryption Standard (DES) algorithm, which is still a mainstay of payment system security.
A Feistel cipher has the ladder structure shown in Figure 5.12. The input is split up into two blocks, the left half and the right half. A round function 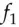 of the left half is computed and combined with the right half using exclusive-or (binary addition without carry), though in some Feistel ciphers addition with carry is also used. (We use the notation
of the left half is computed and combined with the right half using exclusive-or (binary addition without carry), though in some Feistel ciphers addition with carry is also used. (We use the notation  for exclusive-or.) Then, a function
for exclusive-or.) Then, a function 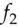 of the right half is computed and combined with the left half, and so on. Finally (if the number of rounds is even) the left half and right half are swapped.
of the right half is computed and combined with the left half, and so on. Finally (if the number of rounds is even) the left half and right half are swapped.
A notation which you may see for the Feistel cipher is 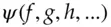 where
where 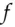 ,
, 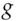 ,
, 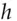 , … are the successive round functions. Under this notation, the above cipher is
, … are the successive round functions. Under this notation, the above cipher is 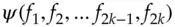 . The basic result that enables us to decrypt a Feistel cipher – and indeed the whole point of his design – is that:
. The basic result that enables us to decrypt a Feistel cipher – and indeed the whole point of his design – is that:
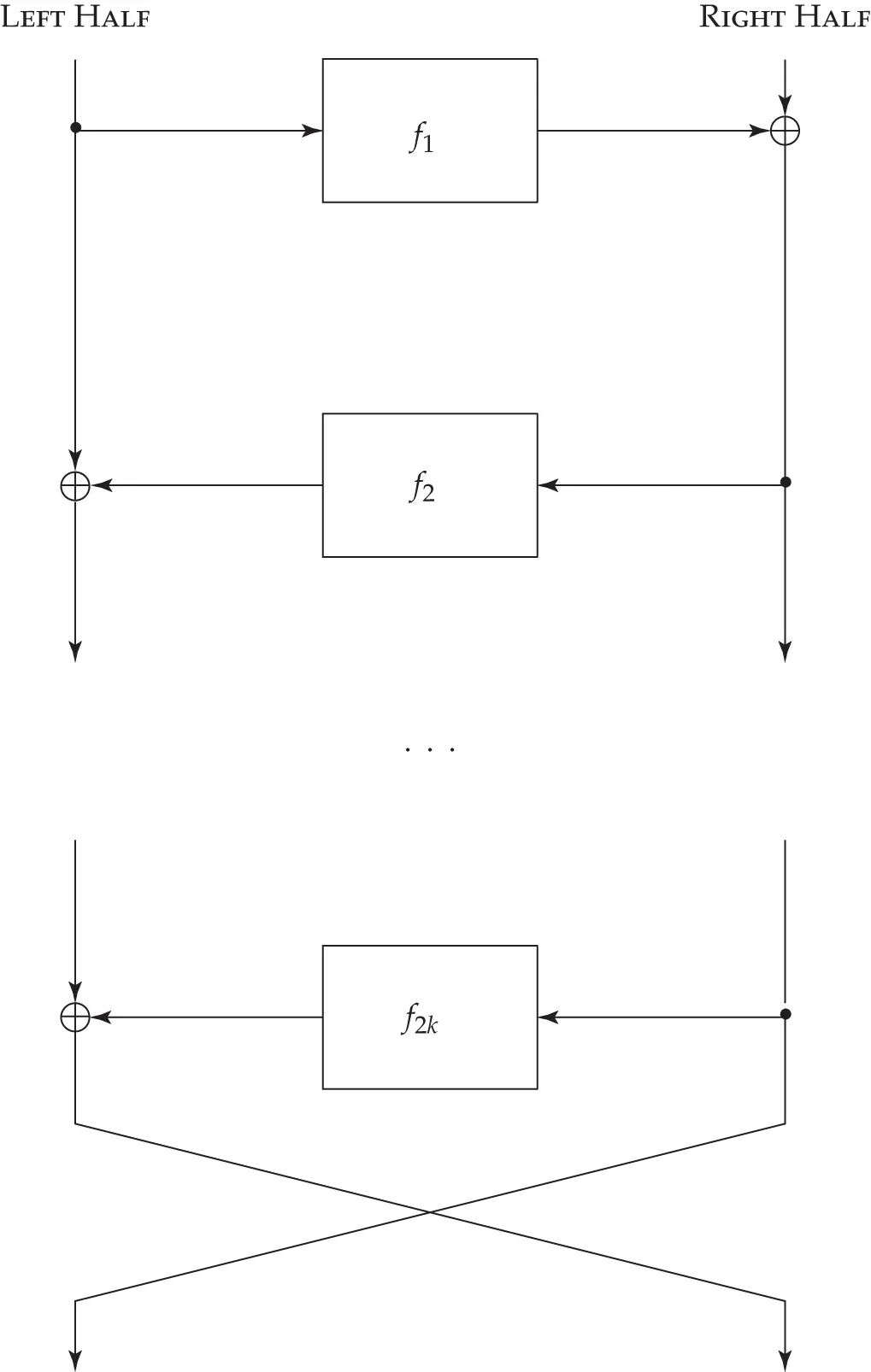
Figure 5.12 : The Feistel cipher structure
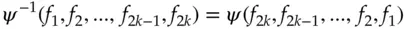
In other words, to decrypt, we just use the round functions in the reverse order. Thus the round functions 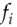 do not have to be invertible, and the Feistel structure lets us turn any one-way function into a block cipher. This means that we are less constrained in trying to choose a round function with good diffusion and confusion properties, and which also satisfies any other design constraints such as code size, software speed or hardware gate count.
do not have to be invertible, and the Feistel structure lets us turn any one-way function into a block cipher. This means that we are less constrained in trying to choose a round function with good diffusion and confusion properties, and which also satisfies any other design constraints such as code size, software speed or hardware gate count.
5.4.3.1 The Luby-Rackoff result
The key theoretical result on Feistel ciphers was proved by Mike Luby and Charlie Rackoff in 1988. They showed that if 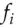 were random functions, then
were random functions, then 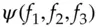 was indistinguishable from a random permutation under chosen-plaintext attack, and this result was soon extended to show that
was indistinguishable from a random permutation under chosen-plaintext attack, and this result was soon extended to show that 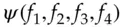 was indistinguishable under chosen plaintext/ciphertext attack – in other words, it was a pseudorandom permutation. (I omit a number of technicalities.)
was indistinguishable under chosen plaintext/ciphertext attack – in other words, it was a pseudorandom permutation. (I omit a number of technicalities.)
In engineering terms, the effect is that given a really good round function, four rounds of Feistel are enough. So if we have a hash function in which we have confidence, it is straightforward to construct a block cipher from it: use four rounds of keyed hash in a Feistel network.
The DES algorithm is widely used in banking and other payment applications. The ‘killer app’ that got it widely deployed was ATM networks; from there it spread to prepayment meters, transport tickets and much else. In its classic form, it is a Feistel cipher, with a 64-bit block and 56-bit key. Its round function operates on 32-bit half blocks and consists of three operations:
first, the block is expanded from 32 bits to 48;
next, 48 bits of round key are mixed in using exclusive-or;
the result is passed through a row of eight S-boxes, each of which takes a six-bit input and provides a four-bit output;
finally, the bits of the output are permuted according to a fixed pattern.
The effect of the expansion, key mixing and S-boxes is shown in Figure 5.13:
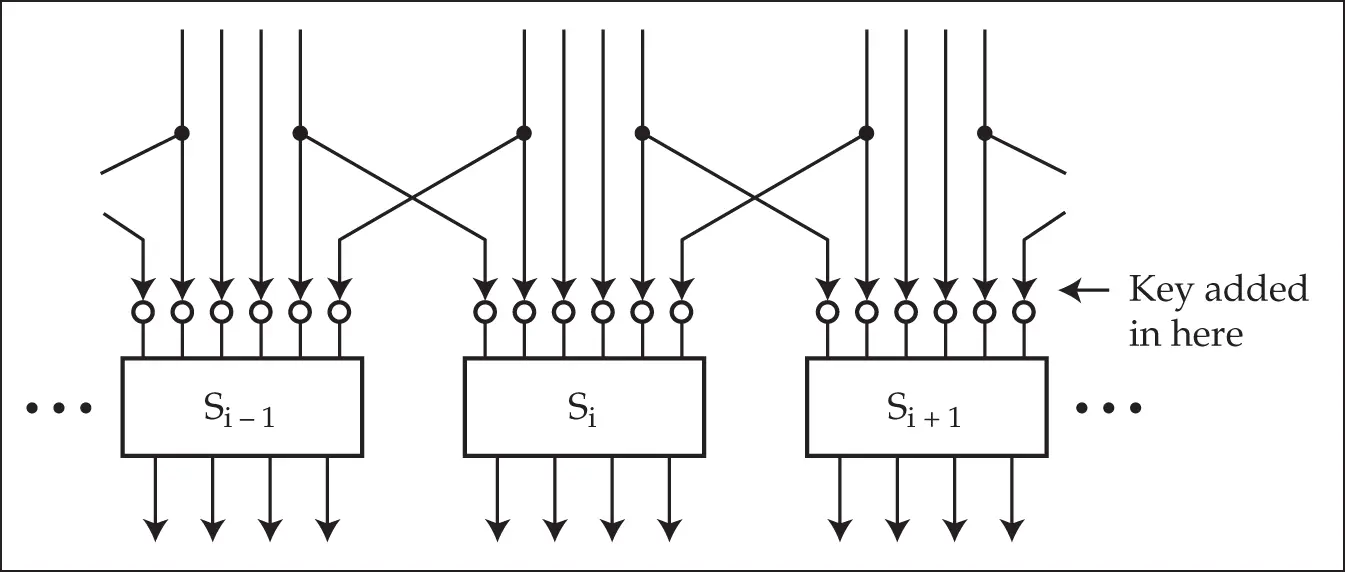
Figure 5.13 : The DES round function
The round keys are derived from the user-supplied key by using each user key bit in twelve different rounds according to a slightly irregular pattern. A full specification of DES is given in [1399].
DES was introduced in 1974 and immediately caused controversy. The most telling criticism was that the key is too short. Someone who wants to find a 56 bit key using brute force, that is by trying all possible keys, will have a total exhaust time of 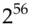 encryptions and an average solution time of half that, namely
encryptions and an average solution time of half that, namely 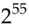 encryptions. Whit Diffie and Martin Hellman argued in 1977 that a DES keysearch machine could be built with a million chips, each testing a million keys a second; as a million is about
encryptions. Whit Diffie and Martin Hellman argued in 1977 that a DES keysearch machine could be built with a million chips, each testing a million keys a second; as a million is about 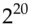 , this would take on average
, this would take on average 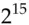 seconds, or a bit over 9 hours, to find the key. They argued that such a machine could be built for $20 million in 1977 [557]. IBM, whose scientists invented DES, retorted that they would charge the US government $200 million to build such a machine. (In hindsight, both were right.)
seconds, or a bit over 9 hours, to find the key. They argued that such a machine could be built for $20 million in 1977 [557]. IBM, whose scientists invented DES, retorted that they would charge the US government $200 million to build such a machine. (In hindsight, both were right.)
During the 1980’s, there were persistent rumors of DES keysearch machines being built by various intelligence agencies, but the first successful public keysearch attack took place in 1997. In a distributed effort organised over the net, 14,000 PCs took more than four months to find the key to a challenge. In 1998, the Electronic Frontier Foundation (EFF) built a DES keysearch machine called Deep Crack for under $250,000, which broke a DES challenge in 3 days. It contained 1,536 chips run at 40MHz, each chip containing 24 search units which each took 16 cycles to do a test decrypt. The search rate was thus 2.5 million test decryptions per second per search unit, or 60 million keys per second per chip. The design of the cracker is public and can be found at [619]. By 2006, Sandeep Kumar and colleagues at the universities of Bochum and Kiel built a machine using 120 FPGAs and costing $10,000, which could break DES in 7 days on average [1110]. A modern botnet with 100,000 machines would take a few hours. So the key length of single DES is now inadequate.
Читать дальше

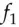 of the left half is computed and combined with the right half using exclusive-or (binary addition without carry), though in some Feistel ciphers addition with carry is also used. (We use the notation
of the left half is computed and combined with the right half using exclusive-or (binary addition without carry), though in some Feistel ciphers addition with carry is also used. (We use the notation  for exclusive-or.) Then, a function
for exclusive-or.) Then, a function 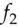 of the right half is computed and combined with the left half, and so on. Finally (if the number of rounds is even) the left half and right half are swapped.
of the right half is computed and combined with the left half, and so on. Finally (if the number of rounds is even) the left half and right half are swapped.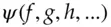 where
where 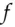 ,
, 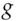 ,
, 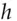 , … are the successive round functions. Under this notation, the above cipher is
, … are the successive round functions. Under this notation, the above cipher is 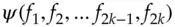 . The basic result that enables us to decrypt a Feistel cipher – and indeed the whole point of his design – is that:
. The basic result that enables us to decrypt a Feistel cipher – and indeed the whole point of his design – is that:
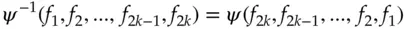
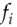 do not have to be invertible, and the Feistel structure lets us turn any one-way function into a block cipher. This means that we are less constrained in trying to choose a round function with good diffusion and confusion properties, and which also satisfies any other design constraints such as code size, software speed or hardware gate count.
do not have to be invertible, and the Feistel structure lets us turn any one-way function into a block cipher. This means that we are less constrained in trying to choose a round function with good diffusion and confusion properties, and which also satisfies any other design constraints such as code size, software speed or hardware gate count.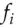 were random functions, then
were random functions, then 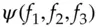 was indistinguishable from a random permutation under chosen-plaintext attack, and this result was soon extended to show that
was indistinguishable from a random permutation under chosen-plaintext attack, and this result was soon extended to show that 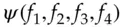 was indistinguishable under chosen plaintext/ciphertext attack – in other words, it was a pseudorandom permutation. (I omit a number of technicalities.)
was indistinguishable under chosen plaintext/ciphertext attack – in other words, it was a pseudorandom permutation. (I omit a number of technicalities.)
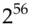 encryptions and an average solution time of half that, namely
encryptions and an average solution time of half that, namely 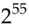 encryptions. Whit Diffie and Martin Hellman argued in 1977 that a DES keysearch machine could be built with a million chips, each testing a million keys a second; as a million is about
encryptions. Whit Diffie and Martin Hellman argued in 1977 that a DES keysearch machine could be built with a million chips, each testing a million keys a second; as a million is about 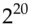 , this would take on average
, this would take on average 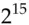 seconds, or a bit over 9 hours, to find the key. They argued that such a machine could be built for $20 million in 1977 [557]. IBM, whose scientists invented DES, retorted that they would charge the US government $200 million to build such a machine. (In hindsight, both were right.)
seconds, or a bit over 9 hours, to find the key. They argued that such a machine could be built for $20 million in 1977 [557]. IBM, whose scientists invented DES, retorted that they would charge the US government $200 million to build such a machine. (In hindsight, both were right.)









