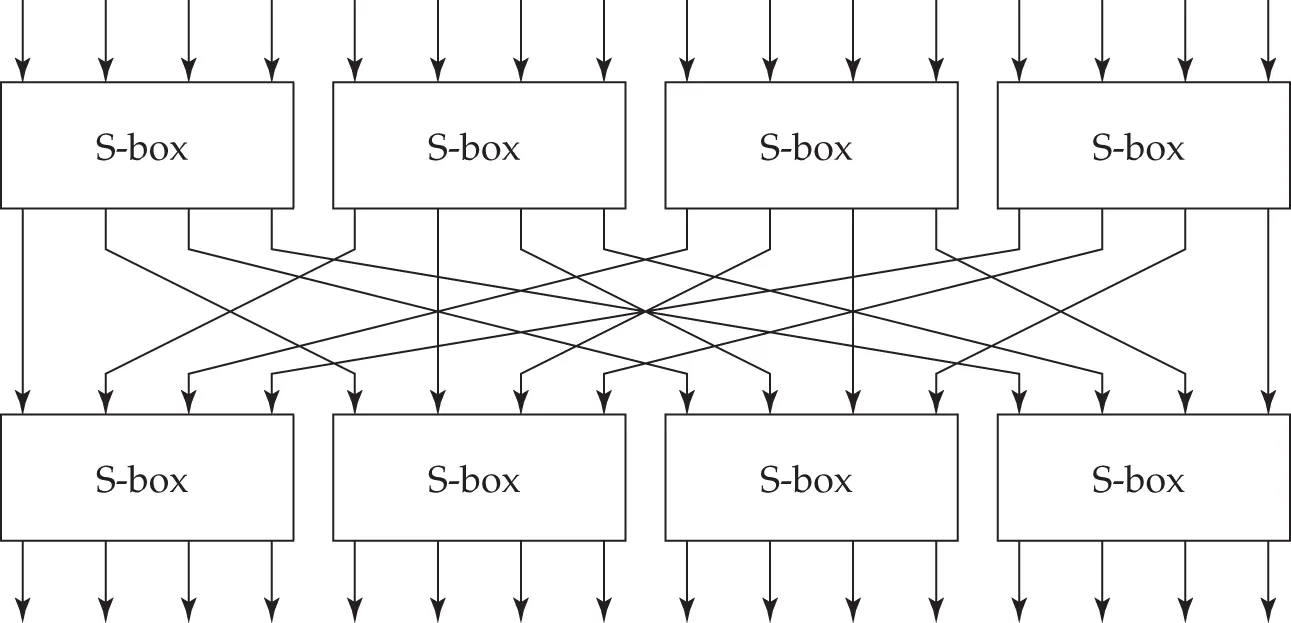
Figure 5.10 : A simple 16-bit SP-network block cipher
Three things need to be done to make such a design secure:
1 the cipher needs to be “wide” enough
2 it needs to have enough rounds, and
3 the S-boxes need to be suitably chosen.
First, a block cipher which operated on sixteen bit blocks would be rather limited, as an opponent could just build a dictionary of plaintext and ciphertext blocks as they were observed. The birthday theorem tells us that even if the input plaintexts were random, he'd expect to find a match as soon as he had seen a few hundred blocks. So a practical block cipher will usually deal with plaintexts and ciphertexts of 64 bits, 128 bits or even more. So if we are using four-bit to four-bit S-boxes, we may have 16 of them (for a 64 bit block size) or 32 of them (for a 128 bit block size).
Second, we have to have enough rounds. The two rounds in Figure 5.10are completely inadequate, as an opponent can deduce the values of the S-boxes by tweaking input bits in suitable patterns. For example, he could hold the rightmost 12 bits constant and try tweaking the leftmost four bits, to deduce the values in the top left S-box. (The attack is slightly more complicated than this, as sometimes a tweak in an input bit to an S-box won't produce a change in any output bit, so we have to change one of its other inputs and tweak again. But it is still a basic student exercise.)
The number of rounds we need depends on the speed with which data diffuse through the cipher. In our simple example, diffusion is very slow because each output bit from one round of S-boxes is connected to only one input bit in the next round. Instead of having a simple permutation of the wires, it is more efficient to have a linear transformation in which each input bit in one round is the exclusive-or of several output bits in the previous round. If the block cipher is to be used for decryption as well as encryption, this linear transformation will have to be invertible. We'll see some concrete examples below in the sections on AES and DES.
5.4.1.3 Choice of S-boxes
The design of the S-boxes also affects the number of rounds required for security, and studying bad choices gives us our entry into the deeper theory of block ciphers. Suppose that the S-box were the permutation that maps the inputs (0,1,2,…,15) to the outputs (5,7,0,2,4,3,1,6,8,10,15,12,9,11,14,13). Then the most significant bit of the input would come through unchanged as the most significant bit of the output. If the same S-box were used in both rounds in the above cipher, then the most significant bit of the input would pass through to become the most significant bit of the output. We certainly couldn't claim that our cipher was pseudorandom.
5.4.1.4 Linear cryptanalysis
Attacks on real block ciphers are usually harder to spot than in this example, but they use the same ideas. It might turn out that the S-box had the property that bit one of the input was equal to bit two plus bit four of the output; more commonly, there will be linear approximations to an S-box which hold with a certain probability. Linear cryptanalysis [897, 1246] proceeds by collecting a number of relations such as “bit 2 plus bit 5 of the input to the first S-box is equal to bit 1 plus bit 8 of the output, with probability 13/16”, then searching for ways to glue them together into an algebraic relation between input bits, output bits and key bits that holds with a probability different from one half. If we can find a linear relationship that holds over the whole cipher with probability 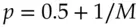 , then according to the sampling theorem in probability theory we can expect to start recovering keybits once we have about
, then according to the sampling theorem in probability theory we can expect to start recovering keybits once we have about 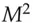 known texts. If the value of
known texts. If the value of 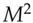 for the best linear relationship is greater than the total possible number of known texts (namely
for the best linear relationship is greater than the total possible number of known texts (namely 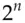 where the inputs and outputs are
where the inputs and outputs are 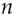 bits wide), then we consider the cipher to be secure against linear cryptanalysis.
bits wide), then we consider the cipher to be secure against linear cryptanalysis.
5.4.1.5 Differential cryptanalysis
Differential Cryptanalysis [246, 897] is similar but is based on the probability that a given change in the input to an S-box will give rise to a certain change in the output. A typical observation on an 8-bit S-box might be that “if we flip input bits 2, 3, and 7 at once, then with probability  the only output bits that will flip are 0 and 1”. In fact, with any nonlinear Boolean function, tweaking some combination of input bits will cause some combination of output bits to change with a probability different from one half. The analysis procedure is to look at all possible input difference patterns and look for those values
the only output bits that will flip are 0 and 1”. In fact, with any nonlinear Boolean function, tweaking some combination of input bits will cause some combination of output bits to change with a probability different from one half. The analysis procedure is to look at all possible input difference patterns and look for those values 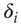 ,
, 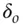 such that an input change of
such that an input change of 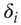 will produce an output change of
will produce an output change of 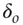 with particularly high (or low) probability.
with particularly high (or low) probability.
As in linear cryptanalysis, we then search for ways to join things up so that an input difference which we can feed into the cipher will produce a known output difference with a useful probability over a number of rounds. Given enough chosen inputs, we will see the expected output and be able to make deductions about the key. As in linear cryptanalysis, it's common to consider the cipher to be secure if the number of texts required for an attack is greater than the total possible number of different texts for that key. (We have to be careful of pathological cases, such as if you had a cipher with a 32-bit block and a 128-bit key with a differential attack whose success probability given a single pair was 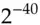 . Given a lot of text under a number of keys, we'd eventually solve for the current key.)
. Given a lot of text under a number of keys, we'd eventually solve for the current key.)
There are many variations on these two themes. For example, instead of looking for high probability differences, we can look for differences that can't happen (or that happen only rarely). This has the charming name of impossible cryptanalysis , but it is quite definitely possible against many systems [243] 4.
Block cipher design involves a number of trade-offs. For example, we can reduce the per-round information leakage, and thus the required number of rounds, by designing the rounds carefully. But a complex design might be slow in software, or need a lot of gates in hardware, so using simple rounds but more of them might have been better. Simple rounds may also be easier to analyse. A prudent designer will also use more rounds than are strictly necessary to block the attacks known today, in order to give some safety margin, as attacks only ever get better. But while we may be able to show that a cipher resists all the attacks we know of, and with some safety margin, this says little about whether it will resist novel types of attack. (A general security proof for a block cipher would appear to imply a result such as 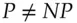 that would revolutionise computer science.)
that would revolutionise computer science.)
Читать дальше


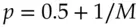 , then according to the sampling theorem in probability theory we can expect to start recovering keybits once we have about
, then according to the sampling theorem in probability theory we can expect to start recovering keybits once we have about 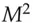 known texts. If the value of
known texts. If the value of 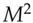 for the best linear relationship is greater than the total possible number of known texts (namely
for the best linear relationship is greater than the total possible number of known texts (namely 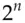 where the inputs and outputs are
where the inputs and outputs are 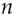 bits wide), then we consider the cipher to be secure against linear cryptanalysis.
bits wide), then we consider the cipher to be secure against linear cryptanalysis. the only output bits that will flip are 0 and 1”. In fact, with any nonlinear Boolean function, tweaking some combination of input bits will cause some combination of output bits to change with a probability different from one half. The analysis procedure is to look at all possible input difference patterns and look for those values
the only output bits that will flip are 0 and 1”. In fact, with any nonlinear Boolean function, tweaking some combination of input bits will cause some combination of output bits to change with a probability different from one half. The analysis procedure is to look at all possible input difference patterns and look for those values 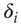 ,
, 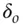 such that an input change of
such that an input change of 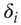 will produce an output change of
will produce an output change of 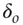 with particularly high (or low) probability.
with particularly high (or low) probability.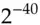 . Given a lot of text under a number of keys, we'd eventually solve for the current key.)
. Given a lot of text under a number of keys, we'd eventually solve for the current key.)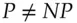 that would revolutionise computer science.)
that would revolutionise computer science.)









