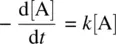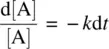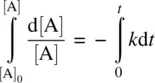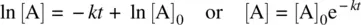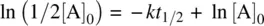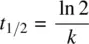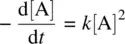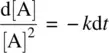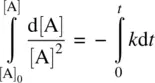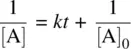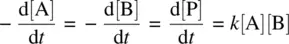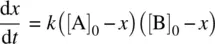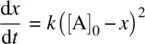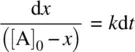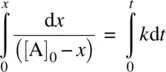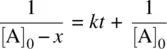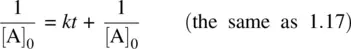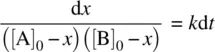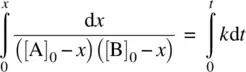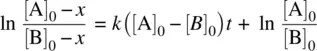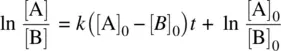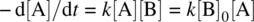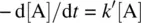Xiaoping Sun - Organic Mechanisms

A unimolecular reaction ( Eq. 1.1: A ➔ P) follows the first‐order rate law as shown in Equation 1.9

(1.9)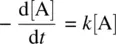

where k is the rate constant(with the typical unit of s −1) for the reaction, and it is independent of the concentration of the reactant. The rate constant is the quantitative measure of how fast the reaction proceeds at a certain temperature.

Rearranging Equation 1.9leads to

(1.10)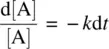

Integrating Equation 1.10on both sides and applying the boundary condition t = 0, [A] = [A] 0(initial concentration), we have

(1.11)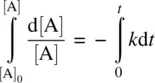

From Equation 1.11, we have ln[A] – ln[A] 0= − kt

Therefore,

(1.12)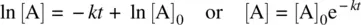

Equation 1.12is the integrated rate law for a unimolecular reaction.

The half‐life ( t 1/2) of reactant A (the time required for conversion of one‐half of the reactant to the product, i.e., when t = t 1/2, [A] = ½ [A] 0) can be solved from Equation 1.12as follows:

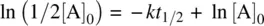
Therefore,

(1.13)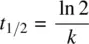

Equation 1.13shows that the half‐life of a substance that undergoes first‐order decay is inversely proportional to the rate constant and independent of the initial concentration.

A bimolecular reaction that involves two reactant molecules of the same compound ( Eq. 1.4: 2A ➔ P) follows the second‐order rate law as shown below:

(1.14)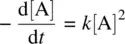

where k is the rate constant (with the typical unit of M −1s −1) for the reaction.

Rearranging Equation 1.14leads to

(1.15)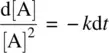

Integrating Equation 1.15on both sides and applying the boundary condition t = 0, [A] = [A] 0(initial concentration), we have

(1.16)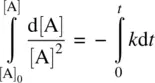

From Equation 1.16, we have

(1.17)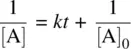

Equation 1.17is the integrated rate law for a bimolecular reaction involving two molecules from the same compound.

A bimolecular reaction that involves two reactant molecules of different compounds ( Eq. 1.5: A + B ➔ P) also follows the second‐order rate law (first‐order in each of the reactants) as shown in Equation 1.18.

(1.18)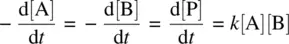

Assume that at a given time t , the molar concentration of the product P is x . Therefore, the molar concentrations of reactants A and B are [A] = [A] 0− x and [B] = [B] 0− x , respectively. [A] 0and [B] 0are initial concentrations of reactants A and B, respectively.

From Equation 1.18, we have

(1.19)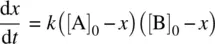

If the quantities of the two reactants A and B are in stoichiometric ratio ([A] 0 = [B] 0 ), Equation 1.19becomes

(1.20)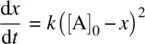

Rearranging Equation 1.20leads to Equation 1.21.

(1.21)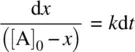

Integrating Equation 1.21on both sides and applying the boundary condition t = 0, x = 0, we have

(1.22)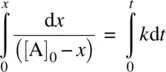

From Equation 1.22, we have

(1.23)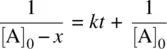

Since [A] = [A] 0− x , Equation 1.23becomes

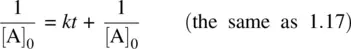
If the reactants A and B have different initial concentrations, Equation 1.19becomes

(1.24)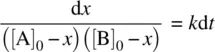

Integrating Equation 1.24on both sides and applying the boundary condition t = 0, x = 0, we have

(1.25)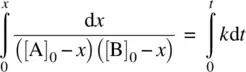

From Equation 1.25, we have

(1.26)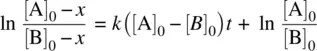

Since [A] = [A] 0− x and [B] = [B] 0− x , Equation 1.26becomes

(1.27)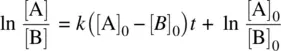

Equation 1.27represents the integrated rate law for a bimolecular reaction involving two different reactant molecules with different initial concentrations.

If one of the reactants (such as B) in Equation 1.5(the bimolecular reaction: A + B ➔ P) is in large excess (typically 10–20‐folds, i.e., [B] 0/[A] 0= 10–20), the change in molar concentration of reactant B in the course of the reaction can be neglected ([B] ~ [B] 0) [2]. The rate law ( Eq. 1.18) becomes

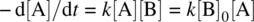
Let k ′ = k [B] 0(the observed rate constant). We have

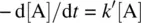
The reaction becomes pseudo first order. The integrated rate law is