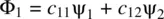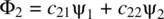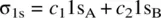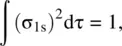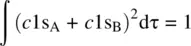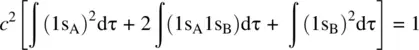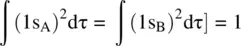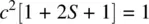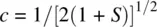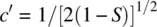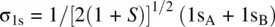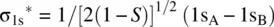Xiaoping Sun - Organic Mechanisms

The microscopic particles such as electrons possess dual properties, which are particle‐like behavior and wave‐like behavior. The latter can be quantitatively characterized by the wavefunction (ψ), which is a function of the space coordinates ( x , y , z in three dimensions) of an electron. The one‐electron wavefunction in an atom is called atomic orbital (AO). The square of a wavefunction (ψ 2) is the probability of finding an electron (also called electron density). The atomic orbitals in the valence shells of the atoms of main group elements include sand porbitals. Their shapes in the three‐dimensional space are illustrated in Figure 1.7.

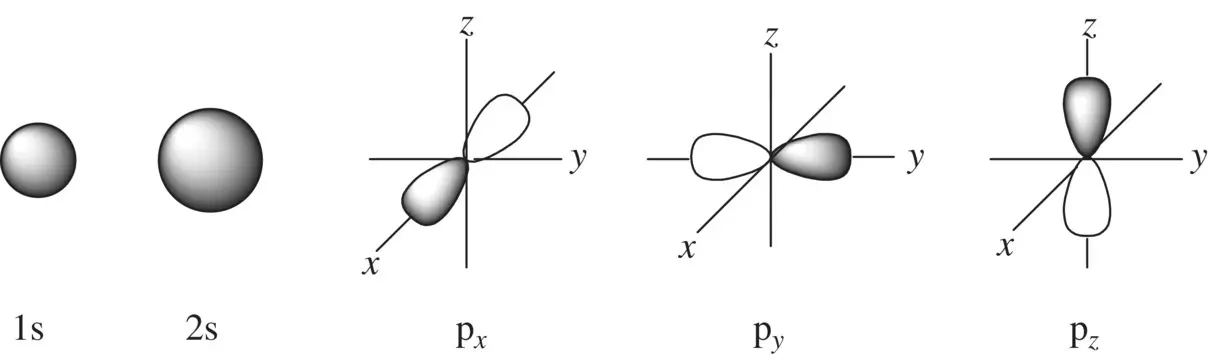
FIGURE 1.7 The shapes of the s and p orbitals in the three‐dimensional space.

Studying the behavior of fundamental particles in chemistry must eventually go beyond the classical laws. It requires that chemical bonding in molecules be explained as a superposition phenomenon of electron wavefunctions. When two atoms (such as hydrogen atoms) approach each other, their valence electrons will start interacting. This makes the wavefunctions (atomic orbitals) of the interacting atoms superimpose (overlap). Mathematically, such a superposition phenomenon (also called orbital overlap) can be expressed in terms of the linear combinations of atomic orbital s ( LCAO s)leading to a set of new wavefunctions in a molecule, called molecular orbital s ( MO s)which are shown in Equations 1.58and 1.59[2].

(1.58)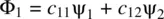

(1.59)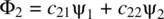

ψ 1and ψ 2represent atomic orbitals of the two approaching atoms 1 and 2, respectively. c 11, c 12, c 21, and c 22are constants (positive, zero, or negative). Φ 1and Φ 2are the resulting molecular orbitals from linear combinations of ψ 1and ψ 2. By the nature, the molecular orbitals are one‐electron wavefunctions. However, they can approximately characterize the behavior of electrons in a many‐electron molecule. In principle, the number of molecular orbitals formed is equal to the number of participating atomic orbitals which overlap in a molecule . In other words, the participating atomic orbitals can combine linearly in different ways. The number of LCAOs is equal to the number of the atomic orbitals.

Figure 1.8illustrates how an H 2molecule is formed from two H atoms. When two H atoms approach to one another, their 1s orbitals (1s Aand 1s B) overlap giving two molecular orbitals σ 1sand σ 1s *through the following linear combinations of 1s Aand 1s B[2].

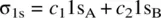
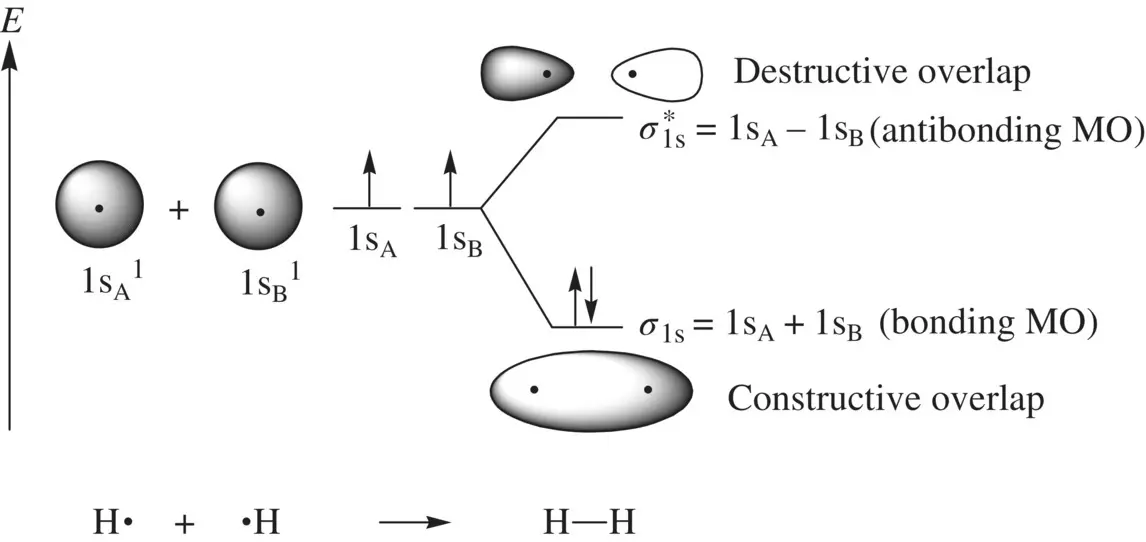
FIGURE 1.8 Formation of the hydrogen molecule (H 2) from two hydrogen (H) atoms.

Since 1s Aand 1s Bare identical, their contributions to each of the MOs (σ 1sand σ 1s *) should be equal. Therefore, we have c 1= c 2= c (>0) and c 1′ = c 2′ = c ′ (>0).

In order to normalize the molecular orbital σ 1s, the following integral must have the value unity

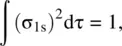
where dτ is the volume factor.

Therefore,

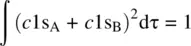
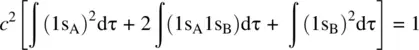
Since the wavefunction of the 1s orbital is normalized, we have

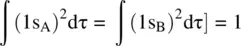
The term S = ∫(1s A1s B)dτ is referred to as the overlap integral. Therefore, we have

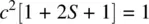
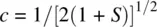
Similarly, by normalizing σ 1s *, we can obtain

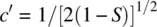
Therefore, we have

(1.60)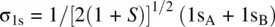

(1.61)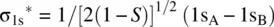

The overlap integral S is determined by the internuclear distance. At equilibrium H─H bond distance, the electron density of σ 1sin the midregion of the bond is maximum, while the electron density of σ 1s *in the midregion of the bond is zero. Therefore, σ 1sis called bonding molecular orbital. It is formed by constructive interaction (overlap) of two atomic orbitals and is responsible for the formation of the H─H σ bond. σ 1s *is called antibonding molecular orbital. It is formed by destructive interaction (overlap) of two atomic orbitals and is responsible for dissociation of the H─H bond. Since each of the 1s orbitals makes the same contribution to the bonding σ 1sand antibonding σ 1s *MOs, the coefficients 1/[2(1 + S)] 1/2and 1/[2(1 − S)] 1/2are often omitted when writing the LCAOs. Therefore, the bonding and antibonding MOs in H 2can be simply written as σ 1s= 1s A+ 1s Band σ 1s *= 1s A− 1s B.

The diatomic halogen X 2(X = F, Cl, Br, or I) molecules are among fundamental main group molecules. Bonding in these molecules, usually represented by F 2, is described in Figure 1.9using MO theory. As two F atoms come together, the two single electrons (in p zorbitals) interact resulting in constructive and destructive orbital overlaps (LCAOs) in the line connecting the two nuclei, giving rise to the formation of the bonding MO (σ 2p= 2p z,A+ 2p z,B) and antibonding MO (σ 2p *= 2p z,A− 2p z,B), respectively.

In the category of nonmetallic main group elements, a π bond is formed by overlap of two p orbitals (LCAOs) in sideways ( Fig. 1.10). If both p orbitals are identical (such as p orbitals in a C=C π bond), each of the p orbitals has the same contribution to the bonding (π p) and antibonding (π p *) MOs ( Fig. 1.10a). They are formed by constructive and destructive sideway orbital overlaps, respectively: π p= p 1+ p 2(fused lobes due to a positive linear combination—constructive orbital overlap) and π p *= p 1− p 2(separated lobes due to a negative linear combination—destructive orbital overlap). If the two p orbitals are from atoms of different elements (such as p orbitals in a C=O π bond), the contribution of each p orbital to the bonding (π p) and antibonding (π p *) MOs is different ( Fig. 1.10b). Usually, the p orbital in the more electronegative atom has greater contribution to the bonding MO (π p), and the p orbital in the less electronegative atom has greater contribution to the antibonding MO (π p *). In the C=O π bond, the bonding (π p) and antibonding (π p *) MOs can be expressed as