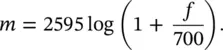Malcolm J. Crocker - Engineering Acoustics

When a masking noise stops, the human hearing system is unable to hear the primary sound signal immediately. This effect is known as postmasking (and is sometimes also known as forward masking.) The time it takes for the primary sound to be heard (normally called the delay time, t d) depends both upon the sound pressure level of the masking noise and its duration. Figure 4.12shows how the primary sound is affected by different sound pressure levels of the masking noise. Also shown in Figure 4.12are dashed lines that correspond to an exponential decay in level with a time constant τ of 10 ms. It is observed that the human hearing mechanism decay is not exponential, but rather that it is nonlinear and that the decay process is complete after a decay time of about 200 ms. This fact is of practical importance since some vehicle and machinery noise is quite impulsive in character such as caused by diesel engines, automobile door closings, brake squeal, warning signals, or impacts that may mask the sounds of speech or other wanted sounds. Figure 4.13shows how sounds are affected by different durations of the masking noise. Figure 4.13presents the level of a just‐audible 2‐kHz test tone as a function of delay time.

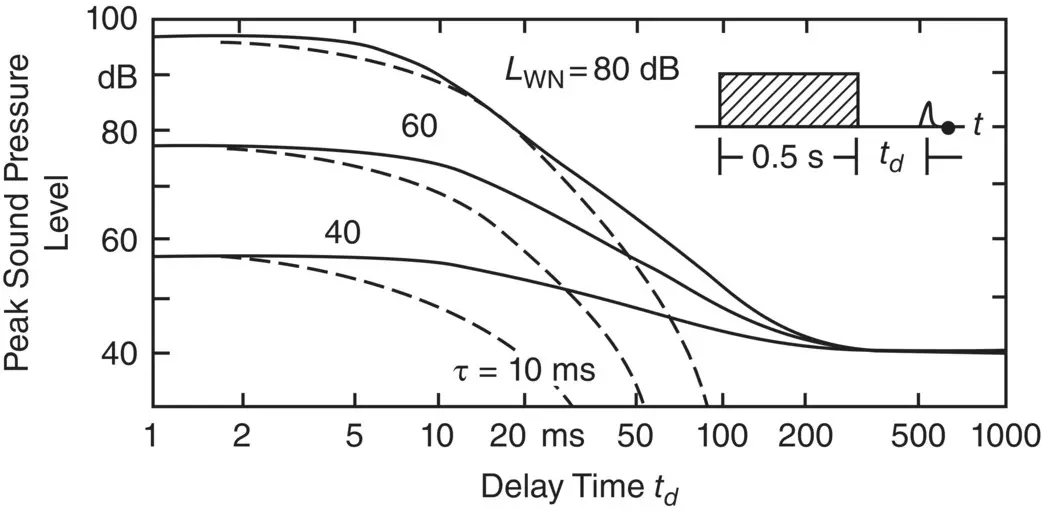
Figure 4.12 Postmasking at different masker sound pressure levels [17].

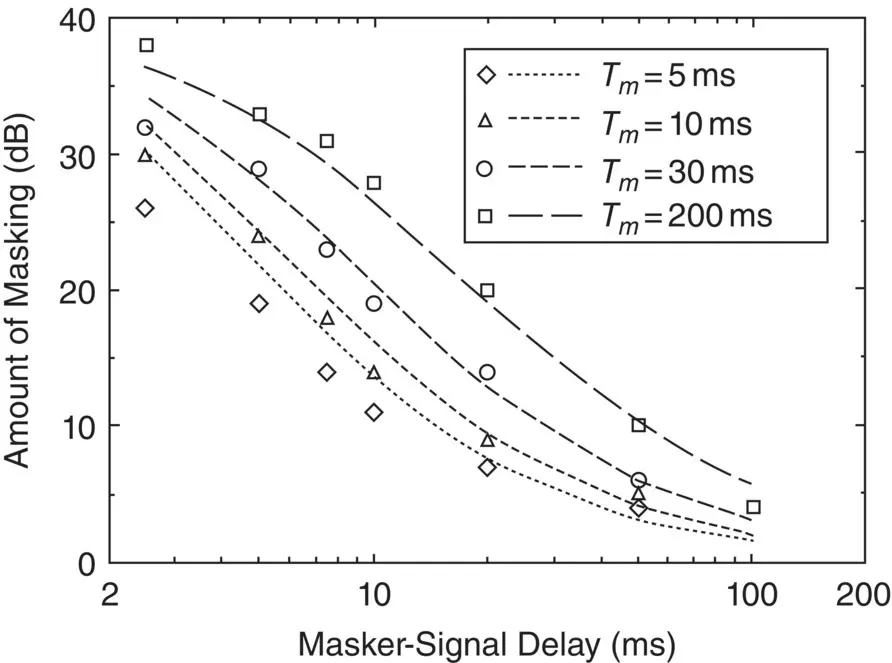
Figure 4.13 Postmasking of 5‐ms, 2‐kHz tones preceded by bursts of uniform masking noise are plotted as a function of the delay between masker and signal offsets. The parameter is masking duration T mas indicated. The symbols are data from Zwicker [31].

Source: Reprinted with permission from [31], American Institute of Physics.

Like loudness ( Section 4.3.2), pitch is another subjective aspect of hearing. Just as people have invented scales to express loudness, others have invented scales for pitch. Stevens et al. [32] were the first to produce a scale in mels. A pure tone of 1000 Hz at a sound pressure level of 40 dB has a pitch of 1000 mels. As a result of subjective experiments, the pitch scale is found to be approximately linear with frequency below 1000 Hz, but approximately logarithmic above 1000 Hz. It has been suggested by some that noise measurements should be made in bands of equal mels (mel was named after the musical term, melody). However, this suggestion has not been adopted. A formula to convert frequency, f (in hertz) into mel, m , is [33]

(4.3)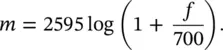

Masking noise may change the pitch of a tone. If the masking noise is of a higher frequency, the pitch of the masked tone is reduced slightly; if the masking noise is of a lower frequency the pitch is increased slightly. This can be explained [34, 35] by a signal/noise ratio argument. The locus of the position on the basilar membrane at which the tone is normally perceived could be changed by the masking noise [34].

What is the equivalent frequency of 2595 mel?

We take the inverse of Eq. (4.3): f = 700(10 m/2595− 1) = 700 (10 − 1) = 6300 Hz.

Figure 4.6in this chapter shows that the ear is most sensitive to sounds in the mid‐frequency range around 1000–4000 Hz. It has a particularly poor response to sound at low frequency. It became apparent to scientists in the 1930s that electrical filters could be designed and constructed with a frequency response approximately equal to the inverse of these equal loudness curves. Thus A‐, B‐, and C‐weighting filters were constructed to approximate the inverse of the 40‐, 70‐, and 90‐phon contours (i.e. for low‐level, moderate, and intense sounds), respectively (see Figure 4.6). In principle, then, these filters, if placed between the microphone and the meter display of an instrument such as a sound level meter, should give some indication of the loudness of a sound (but for pure tones only).

The levels measured with the use of the filters shown in Figure 4.14are commonly called the A‐, B‐, and C‐weighted sound levels. The terminology A‐, B‐, and C‐weighted sound pressure levels is preferred by ISO to reduce any confusion with sound power level and will be used wherever possible throughout this book. The A‐weighting filter has been much more widely used than either the B‐ or C‐weighting filter, and the A‐weighted sound pressure level measured with it is still simply termed by ANSI as the sound level or noise level (unless the use of some other filter is specified). Several other weightings have also been proposed in the past [13]. However, because it is simple, giving a single number, and it can be measured with a low‐cost sound level meter, the A‐weighted sound pressure level has been used widely to give an estimate of the loudness of noise sources such as vehicles, even though these produce moderate to intense noise. Beranek and Ver have reviewed the use of the A‐weighted sound pressure level as an approximate measure of loudness level [36].

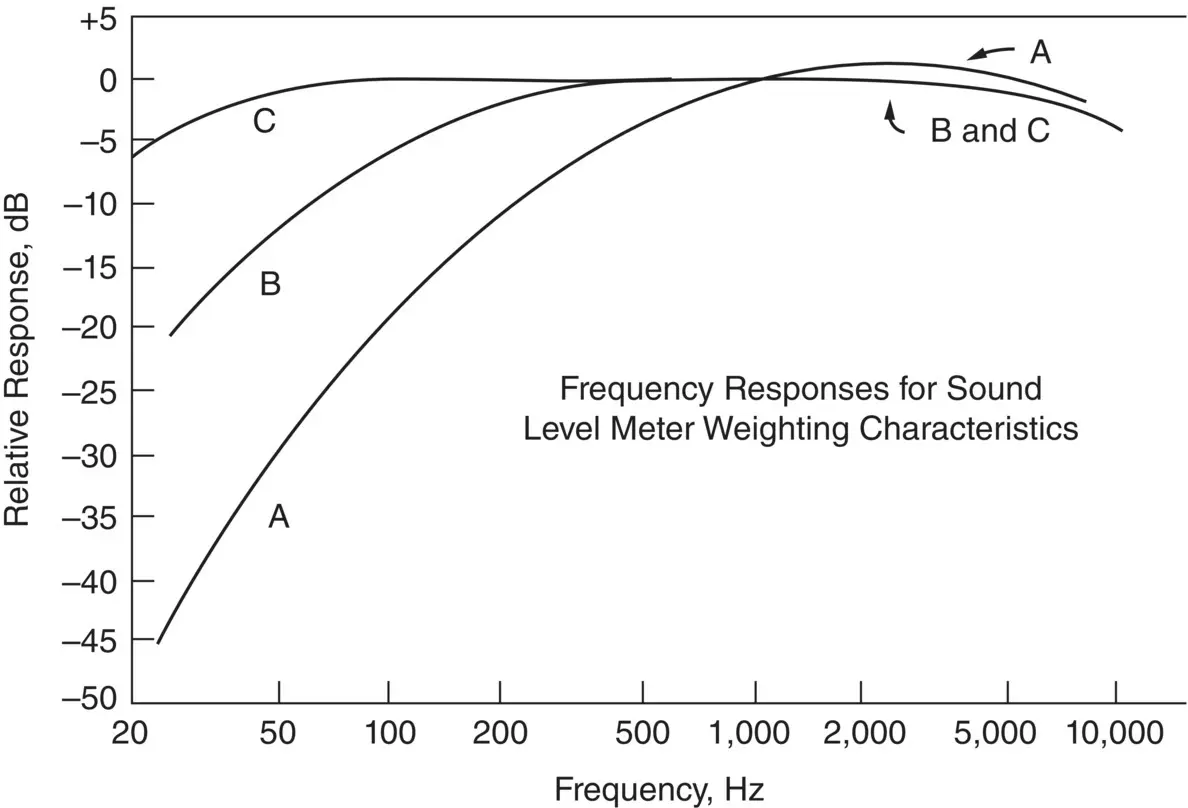
Figure 4.14 A‐, B‐, and C‐weighting filter characteristics used with sound level meters.

The A‐weighted sound pressure levels are often used to gain some approximate measure of the loudness levels of broadband sounds and even of the acceptability of the noise. Figure 4.15shows that there is reasonable correlation between the subjective response of people to vehicle noise and the A‐weighted sound pressure levels measured of the vehicle noise. The A‐weighted sound pressure level forms the basis of many other descriptors for determining human response to noise described later in Chapter 6. The A‐weighted sound pressure level descriptor is also used as a limit for new vehicles ( Chapter 14) and noise levels in buildings ( Chapter 12) in several countries. Although the A‐weighting filter was originally intended for use with low‐level sounds of about 40 dB, it is now commonly used to rate high‐level noise such as in industry where A‐weighted sound pressure levels may exceed 90 dB. At such high levels the A‐weighted sound pressure level and the loudness level are normally in disagreement.

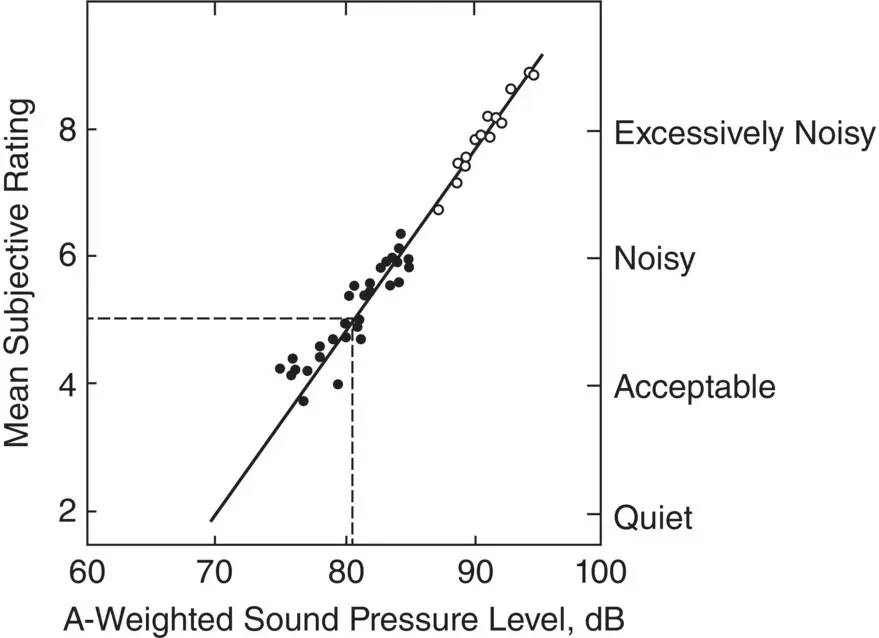
Figure 4.15 Relation between subjective response and A‐weighted sound pressure level for diesel engine trucks undergoing an acceleration test: ●, values measured in 1960, ○, values measured in 1968.

(Source: Adapted from Refs. [37–39].)

The factory noise spectrum (given in Table 4.1), was calculated to have a loudness level of 99 phon (see Example 4.2). Calculate the approximate A‐weighted sound pressure level from the octave band levels given in Table 4.1.

Since we do not have the directly measured A‐weighted sound level, we can calculate this approximately using Figure 4.14. The A‐weighting corrections at the octave band center frequencies have been read off Figure 4.14and entered in Column 3 of Table 4.2. The so‐called A‐weighted octave band sound pressure levels have been calculated in Column 4 and these values have been combined to give the A‐weighted sound pressure level of 89.8, i.e. 90 dB. Note this A‐weighted sound pressure level is dominated by the A‐weighted band levels in the 500, 1000, and 2000 Hz octave bands. These three band levels combine to give 89.5 dB. Similar calculations of the C‐weighted and linear (nonfiltered) sound pressure levels give 91.9 and 92.0 dB, respectively. Thus we see that the A‐weighted sound pressure level is 9 dB below the level in phons and no closer than the linear unweighted sound pressure level of 92 dB. A‐weighted levels should not be used to calculate the loudness level unless the noise is a pure tone – then a good loudness level estimate can be made using the A, B, or C filters (depending on the noise level).