Los geht's!
Vereinfachung durch wissenschaftliche Schreibweise
Die Physik rechnet mit sehr großen und sehr kleinen Zahlen. Um mit diesen Größen umzugehen, verwendet man die wissenschaftliche Schreibweise. Dabei werden Zahlen dargestellt, indem man eine einfache Dezimalzahl mit einer Potenz von 10 multipliziert.
Stellen Sie sich beispielsweise vor, sie müssten die Masse eines Elektrons im MKS-System angeben. Sie legen es auf eine Waage (in Wirklichkeit sind Elektronen zu klein dazu – Sie müssen sehen, wie sie auf magnetische und elektrostatische Kräfte reagieren, wenn Sie ihre Masse bestimmen wollen) und lesen den folgenden Wert ab:
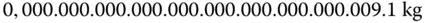
Was um alles in der Welt ist das? Das sind eine Menge Nullen, und sie machen die Zahl zu unhandlich, um mit ihr zu arbeiten. Glücklicherweise wissen Sie alles über die wissenschaftliche Schreibweise und können die Zahl auf die folgende Weise umschreiben:
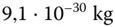
Das ist 9,1 multipliziert mit einer Potenz von 10, nämlich 10 -30. Bei der wissenschaftlichen Schreibweise wird die Zehnerpotenz aus der Zahl herausgezogen, was die Sache gleich viel übersichtlicher macht. Genauer ausgedrückt schreibt man eine Zahl in wissenschaftlicher Schreibweise, indem man die Stellen zählt, die das Komma verschoben werden muss, damit die erste Ziffer links vom Komma steht. Um ein Beispiel zu geben: 0,050 ist 5,0 · 10 -2, da das Komma zwei Stellen nach rechts verschoben wird, um 5,0 zu erhalten. Dagegen schreibt man die Zahl 500 als 5,0 · 10 2, weil man das Komma zwei Stellen nach links verschieben muss, um 5,0 zu erhalten.
Versuchen Sie, die folgenden Fragen zur wissenschaftlichen Schreibweise zu lösen:
 Beispiel
Beispiel
Wie lautet 0,000.037 in wissenschaftlicher Schreibweise?
 Lösung
Lösung
Die richtige Antwort ist 3,7 · 10–5. Sie müssen das Komma fünf Stellen nach rechts verschieben, um 3,7 zu erhalten.
Wie lautet 0,0043 in wissenschaftlicher Schreibweise?
Los geht's!
Wie lautet 430.000,0 in wissenschaftlicher Schreibweise?
Los geht's!
Wie lautet 0,000.000.56 in wissenschaftlicher Schreibweise?
Los geht's!
Wie lautet 6700,0 in wissenschaftlicher Schreibweise?
Los geht's!
Physikalische Aufgaben verlangen häufig das Umrechnen zwischen verschiedenen Maßeinheiten. Wenn man beispielsweise die Anzahl an Metern misst, die ein Spielzeugauto in drei Sekunden zurücklegt, kann man dessen Geschwindigkeit in Metern pro Sekunde angeben. Gebräuchlicher ist allerdings die Angabe in Kilometern pro Stunde, sodass man gegebenenfalls zwischen beiden Einheiten umrechnen muss.
Um ein weiteres Beispiel zu geben: Stellen Sie sich vor, Sie haben 180 Sekunden – wie viele Minuten sind das? Sie wissen, dass eine Minute 60 Sekunden hat, so sind 180 Sekunden das Gleiche wie 3 Minuten.
Hier folgen einige wichtige Umrechnungen zwischen Standardgrößen:
1 m = 100 cm = 1000 mm (Millimeter)
1 km (Kilometer) = 1000 m
1 kg (Kilogramm) = 1000 g (Gramm)
1 N (Newton) = 105 dyn
1 J (Joule) = 107 erg
1 P (Pascal) = 10 bar
1 A (Ampere) = 0,1 Bi
1 T (Tesla) = 104 G (Gauss)
1 C (Coulomb) = 2,9979 · 109 Fr
Der Umrechnungsfaktor zwischen CGS und MKS beträgt meistens 10 oder ein Vielfaches davon, also ist das Umrechnen zwischen beiden Systemen einfach. Aber es gibt auch Einheiten, bei denen die Umrechnung nicht so einfach ist.
Länge:1 Zoll = 2,54 cm1 Meile = 1,609 km1 Å (Ångström) = 10-10 m
Masse:1 u (atomare Masseneinheit, engl. atomic mass unit ) = 1,6605 · 10-27 kg
Energie:1 kWh (Kilowattstunde) = 3,6 · 106 J1 eV (Elektronen Volt) = 1,602 · 10-19 J
Leistung:1 PS (Pferdestärke) = 735,5 W
Weil Umrechnungen in physikalischen Aufgaben so wichtig sind und weil man sie sehr sorgfältig behandeln muss, gibt es dafür auch einen systematischen Weg: Man multipliziert mit einer Umrechnungskonstante, die gleich eins ist, und kürzt die nicht gewünschten Einheiten heraus.
 Beispiel
Beispiel
Ein Ball fällt 5 m. Wie viele cm ist er gefallen?
 Lösung
Lösung
Die richtige Antwort lautet: 500 cm. Um die Umrechnung durchzuführen, stellt man folgende Gleichung auf:
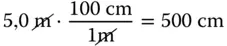
100 cm dividiert durch 1 m ergibt 1, weil 1 m aus 100 cm besteht. In der Gleichung fallen also die Einheiten, die man nicht will – hier zweimal Meter – heraus.
Wie viel cm sind 2,35 m?
Los geht's!
Wie viel s sind 1,25 min?
Los geht's!
Wie viel Zoll sind 2,0 m?
Los geht's!
Wie viel g sind 3,25 kg?
Los geht's!
Manchmal muss man auch mehrere Umrechnungsschritte durchführen, um das gewünschte Ergebnis zu erhalten. Demzufolge benötigt man dann auch mehrere Umrechnungsfaktoren. Wenn man beispielsweise von Zoll in Meter umrechnen will, kann man die Tatsache benutzen, dass 1 Zoll 2,54 Zentimeter enthält – aber anschließend muss man Zentimeter in Meter umrechnen, man muss also noch einen zweiten Umrechnungsfaktor benutzen.
Versuchen Sie sich an diesen Beispielfragen, die mehrere Umrechnungsschritte beinhalten.
 Beispiel
Beispiel
Wie viel m sind 10 Zoll?
 Lösung
Lösung
Die richtige Antwort lautet: 0,254 m.
1 1 Zoll = 2,54 cm, also beginnt man mit dieser Umrechnung und wandelt 10 Zoll in Zentimeter um:
2 Mithilfe eines zweiten Umrechnungsfaktors rechnet man 25,4 cm in m um:
Wie viel Meter sind 17 Meilen?
Los geht's!
Wie viele km sind ein cm?
Los geht's!
Wie viel sind 5 Å in cm?
Los geht's!
Wie viel Zoll sind 1 m, wenn 2,54 cm = 1 Zoll sind (dies ist die exakt festgelegte Umrechnungsformel)?
Los geht's!
Umrechnung von Zeitangaben
Physikalische Aufgaben erfordern häufig das Umrechnen zwischen verschiedenen Maßeinheiten der Zeit: Sekunden, Minuten, Stunden oder auch Jahren. Das führt zu allerlei Umrechnungen, da Messungen in Physikbüchern gewöhnlich in Sekunden, häufig aber auch in Stunden angegeben werden.
Читать дальше

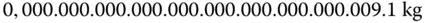
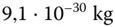
 Beispiel
Beispiel Lösung
Lösung