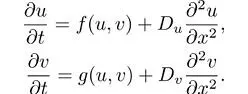Miguel Fuentes - Dinámica científica y medidas de complejidad

Es muy importante notar que, como en casi todos los estudios cuantitativos, el tratamiento habitual de la formación de patrones se realiza mediante el modelamiento de las interacciones macroscópicas [Hoyle, 2006; Cross y Greenside, 2009], ya que en general la escala o longitud del patrón observado es mucho mayor en órdenes de magnitud del tamaño de la interacción microscópica que lo genera (volveré a este punto más adelante, explicando los modelos basados en agentes). Después de discutir la formulación matemática típica del mecanismo de Turing, daremos un ejemplo importante de la aplicación de este modelo en las ciencias sociales.

Morfogénesis y la síntesis de Alan Turing

Algunas de las primeras ideas y descripciones matemáticas sobre cómo los procesos físicos y las limitaciones que afectan el crecimiento biológico –y, por lo tanto, los patrones naturales como las espirales de la filotaxis– fueron descritas por D’Arcy Wentworth Thompson en su bello libro de 1917 On Growth and Form . Allí, Thompson explicó que, bajo su punto de vista, las formas del cuerpo de un animal se crean mediante diferentes velocidades de crecimiento en diversas direcciones. Por ejemplo, al generarse la concha espiral de un caracol. Estos mecanismos eran bastante complicados ya que requerían una mecánica interna muy bien estipulada, y complicada, para producir los diferentes diseños que aparecen por doquier en la naturaleza.

Mucho más tarde, ya entrado el siglo XX, más específicamente en 1952, Alan Turing predijo correctamente un mecanismo de morfogénesis [Turing, 1952], utilizando solamente la difusión de dos señales químicas diferentes: una que activa y otra que desactiva el crecimiento. Este tipo de mecanismos establecen de forma correcta patrones de desarrollo, y solo fueron experimentalmente comprobados décadas después del trabajo teórico de Turing [Castets et al., 1990]. La comprensión más completa de los mecanismos involucrados en los organismos reales requirió el descubrimiento de la estructura del ADN y el desarrollo de la biología molecular y la bioquímica. El modelo de Turing es considerado como una metáfora válida de la morfogénesis biológica, útil para un marco conceptual y para guiar el modelado, pero no para la predicción. Sin embargo, en trabajos muy recientes, se demuestra que el modelo de Turing explica cuantitativamente la morfogénesis en la cual los compartimentos celulares primero se diferencian químicamente y luego físicamente [Sheth et al. 2012; Tompkins et al., 2014].

Es importante para el desarrollo de este trabajo hacer hincapié en lo simple del mecanismo propuesto por Alan Turing. Lo describiremos de manera sucinta a continuación.

La palabra difusión proviene del latín diffudere , que significa extenderse. Hasta la obra de Turing en 1952, la difusión solía considerarse como un mecanismo que homogeneizaba el sistema en el que actuaba. Creemos que otro aporte importante del trabajo de Turing fue demostrar cómo un mecanismo de difusión puede concentrar elementos de un sistema en una región particular (dejando otros con baja concentración), creando así patrones espacio-temporales.

Escribamos una ecuación de reacción-difusión clásica (completa) que describe la inestabilidad de Turing:

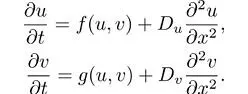
Sigo aquí la discusión simple, y guío a los lectores curiosos a una discusión más formal y completa sobre el tema en las referencias a continuación [Murray, 2002; Cross y Greenside, 2009].

En estas ecuaciones tenemos las partes de reacción: las funciones f(u, v) y g(u, v) y los términos de difusión antes mencionados, caracterizados por dos parámetros de difusión Du y Dv . Una condición necesaria para la inestabilidad de Turing es una diferencia en estos coeficientes de difusión. En particular, la difusión del agente inhibidor, v , debe ser mayor que la del activador u . Con estas condiciones en los parámetros que difunden ambos agentes y detalles un poco más técnicos en las funciones (no lineales) mencionadas f y g , hay un punto de bifurcación donde la solución de esta ecuación cambia de una solución uniforme a una modulada, i. e. una que presenta un patrón.

La utilización exitosa de este tipo de teoría para modelar fenómenos emergentes es notable. En un trabajo reciente, Lim, Metzler y Bar-Yam han estudiado la formación de patrones sociales globales y violencia étnica-cultural [Lim et al., 2007]. Usando un modelo un tanto más sofisticado que el previamente discutido, predicen la emergencia de zonas de conflicto (i. e. los patrones) en Europa del Este con una precisión asombrosa. Este tipo de estudios muestra el poder y la universalidad de estos conceptos y su potencia en la aplicación de esta metodología a diferentes campos de estudio. En términos de teoría de información, se necesitan muy pocos bits de información en el modelo para dar cuenta del fenómeno estudiado.

Hasta ahora hemos discutido modelos continuos. El caso de una red es diferente. Una red es un conjunto de nodos (también llamados vértices) conectados por enlaces [Newman et al., 2011]. La teoría de redes se remonta al célebre problema de puentes de Königsberg y su solución por Euler publicada en 1741, el cual ha sido tratado como el comienzo formal de la teoría de grafos, una teoría matemática que precedió a la teoría de la redes actual. Es muy importante darse cuenta de que hay muchos casos en los que los enfoques del tipo continuo, como el mecanismo de Turing (ver las ecuaciones anteriores), no son una buena aproximación para problemas discretos y solo una visión de red describirá los fenómenos de una manera precisa.

Entre este tipo de sistemas, los cuales han sido de mucha discusión en emergencia actualmente, se encuentran: redes sociales con conexiones entre individuos; las redes de transporte en ciudades o entre ciudades, como por ejemplo las redes de aviones; internet; redes tróficas; redes neuronales; redes de colaboración: científicas, organizaciones o comunidades empresariales, etc.

Hay algunos conceptos importantes que se deben entender cuando se estudian redes, ya que muchos de ellos no solo las caracterizan topológicamente, sino que dan luz sobre los mecanismos que hacen emerger atributos globales. Algunos de estos conceptos son [Costa et al., 2007; Newman, 2010; Gross et al., 2006]:

- Grado: el número de vértices conectados a un nodo. Se puede ver fácilmente la importancia de esta característica, no obstante algunas obras recientes demuestran que algunos nodos con pocos links juegan un papel muy importante en la red global, empalmando distintos “vecindarios” altamente conectados.

- Enlace dirigido, direccionamiento: si una conexión funciona solamente en una dirección, se llama enlace dirigido (pensar, por ejemplo, en un camino de una dirección en una red de transporte).

- Ruta geodésica: es el camino más corto entre dos nodos conectados. Esta cantidad es importante cuando se abordan cuestiones como la propagación de información, el estudio de optimización de rutas o de energía, la propagación de enfermedades infecciosas o similares, etc.

El surgimiento de emergentes en sistemas con capacidad de generar estrategias durante su evolución es uno de los temas fascinantes en el área. En efecto, así lo dan a entender Bedau y Humphreys [2008]:

Además, los procesos evolutivos que dan forma a los linajes biológicos implican emergencia. Una biosfera compleja y altamente diferenciada ha emergido durante miles de millones de años de lo que originalmente era una variedad mucho más simple y mucho más uniforme de las formas de vida temprana.