For Hilbert’s program, the main goal is not only the formalization of Euclidean geometry, but of mathematics as a whole. For him, the most important problem of all mathematics was the foundation of mathematics itself on a solid basis. This meant to Hilbert to reconstruct his own discipline as a purely formal science. This is known as Hilbert’s Formalization Program . He dreamed of presenting all of Mathematics in the same way he had presented Solid Geometry. Any formal system, as Hilbert envisioned it, must have two fundamental properties: Consistency and Completeness . Consistency means that it is not possible to derive within the theory some statement P and its negation. Completeness, on the other hand, means that for each statement P expressible within the system, either P or its negation ¬P can always be derived. Consequently, a formal system is Consistent and Complete if for each statement P expressible within the system, either P or ¬P can be derived from the axioms, but not both. In his Grundlagen der Geometrie , Hilbert proves both the consistency of this axiomatization, and the nonredundancy of the axioms, by constructing models of his system.
1.2 What you will and will not learn in this book
Although this is a book about plane geometry, it only contains very basic results. The most sophisticated results appear in the last chapter, in which many of the propositions of Book I of Euclid’s Elements are proved. For example, you will not find any mention of the Pythagorean theorem. The emphasis is in the rigorous development of the material, following Hilbert’s axiomatic system. Many results are presented which are “intuitively obvious”, and whose proofs are rather involved, pointing out the price one has to pay for deriving everything from the axioms through pure reasoning. In this book you will also learn about plane non-euclidean geometry from the very beginning. This is made possible by the method adopted of thinking of plane geometries as set theoretical structures in which a certain collections of axioms hold.
1.3 Audience prerequisites and style of explanation
This book is essentially self-contained. The only previous knowledge required is high school algebra and the understanding that usual algebraic rules for transforming expressions, and solving equations and inequalities, can actually be derived from the properties of addition, multiplication, exponentiation and order in the real number system. Another prerequisite is of psychological nature: the reader is expected to find delight in rigorous thinking. This is absolutely necessary to enjoy the book. We warn the reader that due to the fact that matters are treated with complete rigor, the reading of arguments quite often may turn painful.
It is important to remark that a deliberate effort was made in presenting algebraic manipulations by what they are, i.e. logical transformations of statements. Let us consider for example the solution process of the equation 5 x − 2 = 2 x + 7 in the real number system. In high school this process is explained as follows:
“Let us solve the equation 5 x − 2 = 2 x + 7. The −2 passes to the +2, and the 2 x passes to the other side as −2 x , obtaining 5 x − 2 x = 7 + 2, which is 3 x = 9. Now since 3 is multiplying on the left hand side, it passes to divide to the right hand side, and so 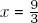 . In this way we see that x = 3”.
. In this way we see that x = 3”.
This is not an explanation at all! This is the application of an algorithm which indeed solves the equation. A good explanation would be as follows:
“Let us solve the equation 5 x −2 = 2 x +7 in the real number system. This means that we want to determine all the possible real numbers x such that five times x minus 2 equals twice x plus 7. Properties of addition and multiplication among real numbers, imply the validity of all the following assertions.
The sentence
“ x is a real number such that 5 x − 2 = 2 x + 7”
is logically equivalent to the sentence
“ x is a real number such that (5 x − 2) + 2 = (2 x + 7) + 2”
(Logical equivalence means that the first sentence implies the second sentence, and that the second sentence implies the first sentence).
Likewise, the sentence
“ x is a real number such that (5 x − 2) + 2 = (2 x + 7) + 2”
is logically equivalent to the sentence
“ x is a real number such that 5 x = 2 x + 9”.
Now, the sentence
“ x is a real number such that 5 x = 2 x + 9”
is logically equivalent to the sentence
“ x is a real number such that 5 x − 2 x = (2 x + 9) − 2 x ”
and this last sentence is logically equivalent to the sentence
“ x is a real number such that 3 x = 9”.
Finally, the sentence
“ x is a real number such that 3 x = 9”
is logically equivalent to the sentence
“ x is a real number such that  ”
”
which is logically equivalent to the sentence
“ x is a real number such that x = 3”.
In conclusion, the sentence
“ x is a real number such that 5 x − 2 = 2 x + 7”
is logically equivalent to the sentence
“ x is a real number such that x = 3”.
But determining all the possible objects x satisfying the latter condition is trivial; only the real number 3 satisfies it. One concludes that x = 3 and no other real number, is such that 5 x − 2 = 2 x + 7.”
We make some remarks about the exercises proposed in the book. They vary in several respects. Some exercises are proposed as the theory is developed. These type of exercises are meant to help understanding the ideas that are being developed. At the end of some sections or strings of sections there are sets of exercises. These exercises are intended to expose the reader to variations of the situations treated in the corresponding section or string of sections. Many times in reading a proof, the reader will find indications like (?), (do it!), (why?), (check!), inviting the reader to reflect or take the corresponding action, about what has just been claimed. Also, some parts of some proofs and examples, are explicitly left as exercises for the reader.
Finally, the book has many, many pictures, for illustrating concepts, steps of proofs, etc. There is a constant effort in presenting two pictures of the same concept, an abstract one and a concrete one, where the plane is taken to be the usual euclidean plane.
Chapter 2is a preliminary chapter, necessary for the understanding of the rest of the book. It starts with a review of the methods for proving statements of the form “ P implies Q ”, and also of methods for proving other types of statements, with particular emphasis on the Induction Method, used for proving statements of the form “ P ( n ) for n ≥ n 0”. Then there is a rapid introduction to the symbolism used in logic. After this the basics of the elementary theory of sets are reviewed, including a discussion of the notion of equivalence relation, and of the important fact that an equivalence relation defined on a set, determines a partition of the set into equivalence classes.
Читать дальше

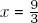 . In this way we see that x = 3”.
. In this way we see that x = 3”. ”
”










