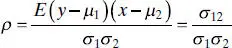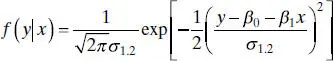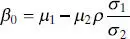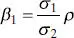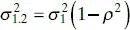(2.58b) 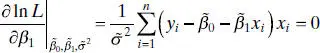
and
(2.58c) 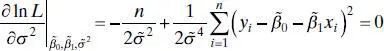
The solution to Eq. (2.58)gives the maximum-likelihood estimators:
(2.59a) 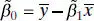
(2.59b) 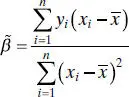
(2.59c) 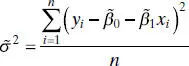
Notice that the maximum-likelihood estimators of the intercept and slope, 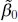 and
and 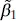 , are identical to the least-squares estimators of these parameters. Also,
, are identical to the least-squares estimators of these parameters. Also, 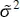 is a biased estimator of σ 2. The biased estimator is related to the unbiased estimator
is a biased estimator of σ 2. The biased estimator is related to the unbiased estimator 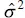 [ Eq. (2.19)] by
[ Eq. (2.19)] by 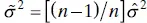 . The bias is small if n is moderately large. Generally the unbiased estimator
. The bias is small if n is moderately large. Generally the unbiased estimator 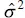 is used.
is used.
In general, maximum-likelihood estimators have better statistical propertiesthan least-squares estimators. The maximum-likelihood estimators are unbiased(including 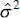 , which is asymptotically unbiased, or unbiased as n becomes large) and have minimum variancewhen compared to allother unbiased estimators. They are also consistent estimators(consistency is a large-sample property indicating that the estimators differ from the true parameter value by a very small amount as n becomes large), and they are a set of sufficient statistics(this implies that the estimators contain all of the “information” in the original sample of size n ). On the other hand, maximum-likelihood estimation requires more stringent statistical assumptions than the least-squares estimators. The least-squares estimators require only second-moment assumptions (assumptions about the expected value, the variances, and the covariances among the random errors). The maximum-likelihood estimators require a full distributional assumption, in this case that the random errors follow a normal distribution with the same second moments as required for the least- squares estimates. For more information on maximum-likelihood estimation in regression models, see Graybill [1961, 1976], Myers [1990], Searle [1971], and Seber [1977].
, which is asymptotically unbiased, or unbiased as n becomes large) and have minimum variancewhen compared to allother unbiased estimators. They are also consistent estimators(consistency is a large-sample property indicating that the estimators differ from the true parameter value by a very small amount as n becomes large), and they are a set of sufficient statistics(this implies that the estimators contain all of the “information” in the original sample of size n ). On the other hand, maximum-likelihood estimation requires more stringent statistical assumptions than the least-squares estimators. The least-squares estimators require only second-moment assumptions (assumptions about the expected value, the variances, and the covariances among the random errors). The maximum-likelihood estimators require a full distributional assumption, in this case that the random errors follow a normal distribution with the same second moments as required for the least- squares estimates. For more information on maximum-likelihood estimation in regression models, see Graybill [1961, 1976], Myers [1990], Searle [1971], and Seber [1977].
2.13 CASE WHERE THE REGRESSOR x IS RANDOM
The linear regression model that we have presented in this chapter assumes that the values of the regressor variable x are known constants. This assumption makes the confidence coefficients and type I (or type II) errors refer to repeated sampling on y at the same x levels. There are many situations in which assuming that the x ’s are fixed constants is inappropriate. For example, consider the soft drink delivery time data from Chapter 1( Figure 1.1). Since the outlets visited by the delivery person are selected at random, it is unrealistic to believe that we can control the delivery volume x . It is more reasonable to assume that both y and x are random variables.
Fortunately, under certain circumstances, all of our earlier results on parameter estimation, testing, and prediction are valid. We now discuss these situations.
2.13.1 x and y Jointly Distributed
Suppose that x and y are jointly distributed random variables but the form of this joint distribution is unknown. It can be shown that all of our previous regression results hold if the following conditions are satisfied:
1 The conditional distribution of y given x is normal with conditional mean β0 + β1x and conditional variance σ2.
2 The x’s are independent random variables whose probability distribution does not involve β0, β1, and σ2.
While all of the regression procedures are unchanged when these conditions hold, the confidence coefficients and statistical errors have a different interpretation. When the regressor is a random variable, these quantities apply to repeated sampling of ( xi , yi ) values and not to repeated sampling of yi at fixed levels of xi .
2.13.2 x and y Jointly Normally Distributed: Correlation Model
Now suppose that y and x are jointly distributed according to the bivariate normal distribution. That is,
(2.60) 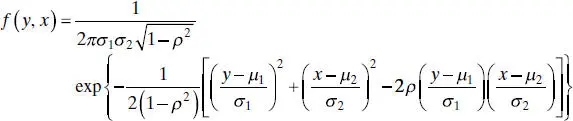
where μ 1and 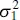 the mean and variance of y , μ 2and
the mean and variance of y , μ 2and 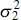 the mean and variance of x , and
the mean and variance of x , and
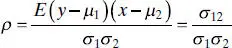
is the correlation coefficientbetween y and x . The term σ 12is the covarianceof y and x .
The conditional distributionof y for a given value of x is
(2.61) 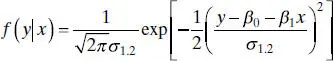
where
(2.62a) 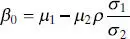
(2.62b) 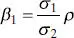
and
(2.62c) 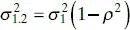
Читать дальше

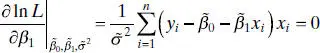
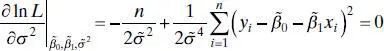
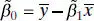
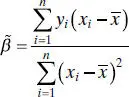
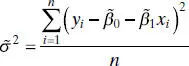
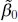 and
and 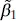 , are identical to the least-squares estimators of these parameters. Also,
, are identical to the least-squares estimators of these parameters. Also, 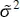 is a biased estimator of σ 2. The biased estimator is related to the unbiased estimator
is a biased estimator of σ 2. The biased estimator is related to the unbiased estimator 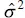 [ Eq. (2.19)] by
[ Eq. (2.19)] by 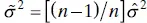 . The bias is small if n is moderately large. Generally the unbiased estimator
. The bias is small if n is moderately large. Generally the unbiased estimator 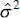 , which is asymptotically unbiased, or unbiased as n becomes large) and have minimum variancewhen compared to allother unbiased estimators. They are also consistent estimators(consistency is a large-sample property indicating that the estimators differ from the true parameter value by a very small amount as n becomes large), and they are a set of sufficient statistics(this implies that the estimators contain all of the “information” in the original sample of size n ). On the other hand, maximum-likelihood estimation requires more stringent statistical assumptions than the least-squares estimators. The least-squares estimators require only second-moment assumptions (assumptions about the expected value, the variances, and the covariances among the random errors). The maximum-likelihood estimators require a full distributional assumption, in this case that the random errors follow a normal distribution with the same second moments as required for the least- squares estimates. For more information on maximum-likelihood estimation in regression models, see Graybill [1961, 1976], Myers [1990], Searle [1971], and Seber [1977].
, which is asymptotically unbiased, or unbiased as n becomes large) and have minimum variancewhen compared to allother unbiased estimators. They are also consistent estimators(consistency is a large-sample property indicating that the estimators differ from the true parameter value by a very small amount as n becomes large), and they are a set of sufficient statistics(this implies that the estimators contain all of the “information” in the original sample of size n ). On the other hand, maximum-likelihood estimation requires more stringent statistical assumptions than the least-squares estimators. The least-squares estimators require only second-moment assumptions (assumptions about the expected value, the variances, and the covariances among the random errors). The maximum-likelihood estimators require a full distributional assumption, in this case that the random errors follow a normal distribution with the same second moments as required for the least- squares estimates. For more information on maximum-likelihood estimation in regression models, see Graybill [1961, 1976], Myers [1990], Searle [1971], and Seber [1977].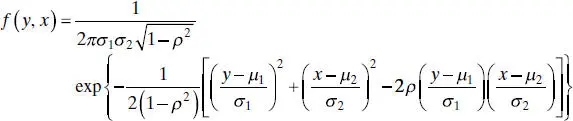
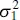 the mean and variance of y , μ 2and
the mean and variance of y , μ 2and 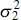 the mean and variance of x , and
the mean and variance of x , and