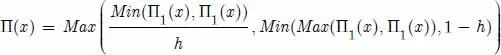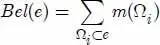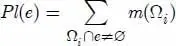Mechanical Engineering in Uncertainties From Classical Approaches to Some Recent Developments

[1.19]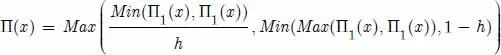

These three modes of combination usually make it possible to combine distributions of possibility from different sources (experts, for example). If there is good agreement between the sources (for example, trapezoidal distributions with overlapping cores), then either the connective or disjunctive modes are both well suited. The choice between the two depends on whether one wishes to consider only consensus or whether one wishes to integrate divergent views as well.

In the absence of good agreement between sources (for example, trapezoidal distributions with non-overlapping kernels), the conjunctive and disjunctive modes are less well suited. The disjunctive mode introduces a multimodal distribution (two peaks), which is generally not desirable in terms of quantifying and propagating uncertainties. The conjunctive mode by itself is too limiting, as it only considers consensus, which can be very limited or even null. The intermediate mode is a proposed solution to resolve these two problems associated with the conjunctive and disjunctive modes. It should be noted that variations on the intermediate mode have also been proposed in order to give more confidence to one distribution (in other words, an expert) than to another. The reader may refer to Dubois and Prade (1992) for more information.

The theory of belief functions (or evidence theory) is another theory for modeling uncertainties of an epistemic nature. It was developed by Dempster (1967) and Shafer (1976) and is consequently sometimes known as the Demspter–Shafer theory. This approach is similar in spirit to the probability box theory and possibility theory, in that it seeks to obtain a bounding for a CDF.

Formally, evidence theory is defined on a belief space EE defined as follows:

DEFINITION 1.20.– Let Ω be a set and E the set of the subsets of Ω. A function m : E → ℝ is called belief mass function if it satisfies the following axioms:

– the function has values between 0 and 1: ∀A ∈ E,0 ≤ m(A) ≤ 1;

– the image of the empty set is 0: m(∅) = 0;

– the image of all the events in the universe is 1:m(Ω) = 1;

– the sum of the masses of the events of E is 1: ∀An ∈ E,

DEFINITION 1.21.– Let Ω be a set, called universe, E the set of subsets of Ω and m a belief mass function . The triplet ( Ω, E, m) is called the belief space EE .

Note that the belief mass function m provides, as was the case for the possibility distribution, a measure of the relative likelihood of each element of E . In the terminology of the theory of belief functions, an element of E that has a non-zero mass is called a focal element, denoted Ω i. Note that these focal elements are, most of the time, defined such as to form a set of disjoint elements. The quantity mi = m (Ω i) is then called mass (or sometimes basic probability assignment [BPA]) associated with this focal element.

In order to be able to compare the likelihood of different events, two quantities, plausibility and belief of the event, are introduced.

DEFINITION 1.22.– Let ( Ω, E, m) be a belief space. We call belief (noted Bel) and plausibility (denoted Pl) of an event e ∈ E, respectively:

[1.20]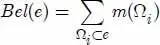

[1.21]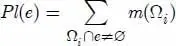

From a conceptual point of view, the mass of a focal element m (Ω i) provides the true likelihood that is attributed to that focal element, but without specifying how this likelihood is distributed among the subsets of Ω i . Therefore, the belief Bel(e) of an event e represents the minimal likelihood that can be associated with e , while the plausibility Pl(e) represents the maximum likelihood that can be associated with e .

In the vast majority of applications of evidence theory, focal elements are defined such as to form a set of adjacent polytopes (or even orthotopes). To illustrate this, consider a universe with nine focal elements Ω 1 to Ω 9 of mass m1 to m9 (see Figure 1.11). Let us now consider the belief and plausibility of the event e , shaded in the figure. According to the definition, the plausibility Pl ( e ) is obtained by adding the masses of the focal elements that have a non-zero intersection with e (in our case Ω 2 , Ω 3 , Ω 5 , Ω 6 , Ω 8 and Ω 9 ). This means that each focal point included even partially in e contributes to the plausibility of e . The belief Bel ( e ) is calculated by summing only the masses of the focal elements entirely included in e (in our case, Ω 3 and Ω 6 ). Belief and plausibility can thus be seen as a bounding for the likelihood of an event, reflecting the fact that the distribution of likelihood within a focal element is not known, due to epistemic uncertainty. By considering Ω 8 we can, for example, consider that the likelihood of the small gray triangle included in Ω 8 is very low and that the mass m8 thus contributes almost nothing to the likelihood of e . This hypothesis comes closer to the calculation of belief. On the other hand, we can also assume that all the likelihood of Ω 8 is concentrated in this small gray triangle and all the rest of Ω 8 is not at all likely. In this case, m8 must actually contribute in full to the likelihood of e . This assumption is thus close to the plausibility calculation. Both cases are thus extreme cases, bounding the true likelihood.

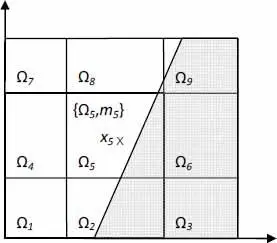
Figure 1.11. Example of an uncertainty structure (focal elements Ωi of mass mi) in the theory of belief functions. An event e is grayed out here

Note that, in a similar way to what has been done in probability and possibility theory, a cumulative plausibility function (CPlF), a cumulative belief function (CBF), a complementary cumulative plausibility function (CCPlF) and a complementary cumulative belief function (CCBF) can be associated with a BPA function. Figure 1.12illustrates these different functions in an example where a BPA function assigns a mass of 0.1 to the following intervals: [1,3], [1,4], [1,10], [2,4], [2,6], [5,8], [5,10], [7,8], [7,10], [9,10].

Note that, while the curves in Figures 1.7and 1.12are similar in terms of their stepwise nature, there are some notable differences. The major difference is that in possibility theory, the necessity must be zero for the possibility to be different from 1 and vice versa. Such a constraint does not exist in evidence theory, which allows plausibility and belief to be simultaneously different from 0 and 1. This thus allows for a much narrower bounding of an unknown cumulative probability function than could be achieved in possibility theory.