Mechanical Engineering in Uncertainties From Classical Approaches to Some Recent Developments

This section aims to highlight the commonalities and differences between probability and possibility theories. First of all, in terms of axioms, the main difference lies in terms of σ-additivity for probability theory and subadditivity for possibility theory (see the definitions given in sections 1.3.1and 1.7.1). Let us recall that the probability of the union of disjoint events is equal to the sum of the probabilities of the events. Thus, if {A 1, …, A n } is a partition of the universe, then the sum of the probabilities of the A imust be equal to 1. There is no similar constraint in terms of possibilities of events Ai. For example, the sum of the probabilities of the events “tomorrow it will snow” and “tomorrow it will not snow” must be equal to 1. On the other hand, if we assign a possibility of 0.7 to “it will snow tomorrow”, we must assign a possibility of 1 to the event “it will not snow tomorrow”. This is because the maximum possibility in the universe must be equal to 1. Thus, since the possibility of the universe Ω is the maximum possibility of the events in the universe, this implies that the possibility of at least one event in the partition must be equal to 1.

Both probability theory and possibility theory work with distribution functions, called PDF in the probabilistic framework and PoDF within the possibility framework. However, despite visual similarities, these two functions account for significantly different modeling. Figure 1.8illustrates some of these differences.

We can see the following differences in Figure 1.8:

– the area under the probability density curve provides the probability of the corresponding event while the area under the curve of a PoDF has no significance;

– in the case of (absolutely) continuous random variables the probability of the variable taking a specific value is zero, while the possibility of the same event can be any value between 0 and 1;

– the area under the curve of a PDF must be 1 while its maximum can be any value. The converse is true for a PoDF;

– the interval between two points with a possibility α corresponds to an α-cut and represents the subset with a possibility at least equal to α. There is no equivalent meaning in probability theory.

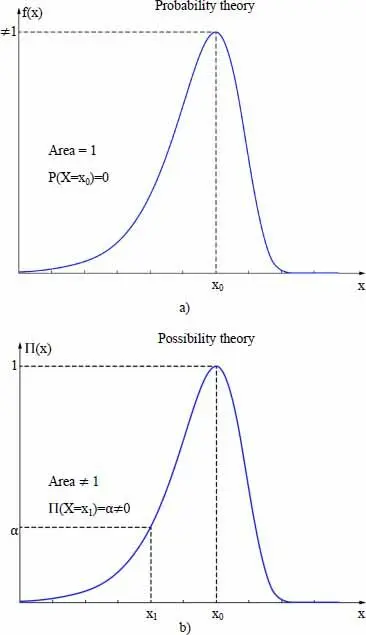
Figure 1.8. Comparison between a probability density function f(x) and a possibility distribution function Π (x)

In order to ensure consistency between variables modeled in a probabilistic manner and variables modeled in a possibilistic manner, the following condition is typically imposed: the possibility of an event must be greater than or equal to its probability. This is consistent with the usual meaning of the words probable and possible: when we say “it is probable that it will snow tomorrow”, this shows a stronger conviction than when we say “it is possible that it will snow tomorrow”. This condition of consistency implies that reasoning in terms of possibilities is more conservative than reasoning in terms of probabilities.

The differences in the probabilistic and possibilistic axioms, as well as the consistency requirement specified above, imply a very different interpretation of distribution functions (CDF or CPoF) in these two frameworks. Let us examine how the two theories model the information X in the interval [8,12]. If we want to model this in a purely probabilistic framework (and not in a context of probability boxes), we need to make an additional assumption, such as the principle of indifference between values in this interval, which leads to modeling by a uniform distribution between 8 and 12. The corresponding probability density is shown in Figure 1.9. The figure also represents a PoDF modeling the same information ( X is in the interval [8,12]). Note that multiple possibility distributions could have been plotted. In particular, a uniform distribution with a possibility value of 1 might have been suitable. Such a distribution would have been very conservative, being the most uninformative distribution that could have been constructed. On the other hand, the triangular distribution plotted in Figure 1.9is the most informative distribution that can be plotted and at the same time meets the consistency condition, which requires that the possibility of any event X be greater than or equal to its probability.

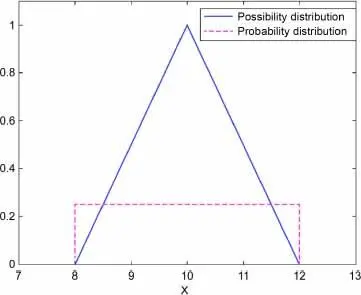
Figure 1.9. Probability density function and possibility distribution function satisfying the consistency condition

To conclude this comparison, it should be noted that possibility and necessity can be considered as upper and lower bounds of true probability in the presence of epistemic uncertainty. This implies that the cumulative functions of possibility (CPoF) and necessity (CNeF) will bound the cumulative probability distribution function (CDF).

This is illustrated in Figure 1.10for the previous example of the variable X within the range [8,12]. The CPF of the uniform probability distribution is effectively bounded by the CPoF and the CNeF. This bounding models the presence of epistemic uncertainty. Indeed, the statement X in the interval [8,12] is very vague and many probability distributions could have been suitable. We had to introduce the principle of indifference, which may be debatable, to obtain the uniform distribution and its associated CDF. In the absence of this assumption, any PDF whose CDF would have been between the CPoF and CNeF curves could have been suitable. The CPoF and CNeF bounding is thus similar in spirit to that obtained in the context of probability boxes ( p-boxes ), but obtained within the context of possibility theory, based on axioms that are quite different from those of probability theory.

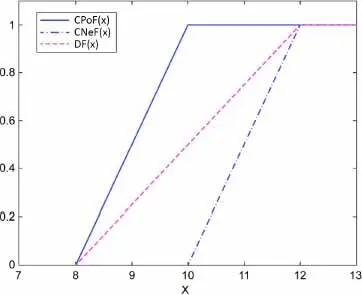
Figure 1.10. Distribution function (DF), cumulative possibility function (CPoF) and cumulative necessity function (CNeF). For a color version of this figure, see www.iste.co.uk/gogu/uncertainties.zip

Possibility theory addresses the problem of quantifying uncertainties when solely based on expert opinion, which will assign likelihood levels to different values of the quantity of interest via possibility distributions Π( x ) (typically via triangular or trapezoidal distributions). One of the fundamental questions that then arises is how to deal with divergent expert opinions. For this purpose, different rules for combining possibility distributions have been established.

Let Π 1and Π 2be two possibility distributions. These distributions can be aggregated according to the following rules:

– the conjunctive mode: this is the equivalent of the intersection of events. It corresponds to retaining only the consensus (the common area under the two distributions). This consensus is typically renormalized in order to satisfy the possibilistic axioms;

– the disjunctive mode: this is the equivalent of the union of events. It corresponds to the union of the two distributions;

– the intermediate mode (proposed by Dubois and Prade 1992): as its name indicates, this is an intermediate mode between the two previous ones. By defining the consensus, that is, the upper possibility bound following the intersection of the two distributions, by h, the distribution of the intermediate mode is defined by: