– C-boxes: this approach can be seen as an extension of the confidence bands making it possible to work on structures modeling all levels of confidence at the same time.
Probability box-based approaches have been applied in many areas of engineering. In the context of mechanics, we can cite the application to the analysis of the buckling load of the Ariane 5 fairing (Oberguggenberger et al . 2009). Roy and Balch (2012) applied probability boxes for predicting the thrust of a supersonic nozzle, while Zhang et al . (2011) applied them to the analysis of a finite element lattice.
Probability boxes-based approaches are generally well suited for analyses where aleatory and epistemic uncertainties are simultaneously present. Its major disadvantage lies in the difficulty of obtaining bounding functions 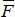 and F in practice, especially in the presence of small amounts of data (a small number of samples or even no samples at all and only the availability of expert opinions, etc.). Indeed, when few samples are available, the bounding that can usually be obtained on the distribution function is too large to be useful in practice. Sometimes there is even a total absence of samples (that is, there have been no formalized experiments that can be traced and exploited) and only expert opinions can provide information on existing uncertainties. How can the bounds
and F in practice, especially in the presence of small amounts of data (a small number of samples or even no samples at all and only the availability of expert opinions, etc.). Indeed, when few samples are available, the bounding that can usually be obtained on the distribution function is too large to be useful in practice. Sometimes there is even a total absence of samples (that is, there have been no formalized experiments that can be traced and exploited) and only expert opinions can provide information on existing uncertainties. How can the bounds 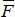 and F be constructed based on these expert opinions? Various approaches, which we shall review later, and, in particular, the Dempster–Shafer theory, which is conceptually quite close to probability boxes, have sought to overcome these difficulties.
and F be constructed based on these expert opinions? Various approaches, which we shall review later, and, in particular, the Dempster–Shafer theory, which is conceptually quite close to probability boxes, have sought to overcome these difficulties.
As we have seen in previous sections, one of the major problems in modeling epistemic uncertainties resides in the determination of the probability distribution (or its bounding) that a certain physical quantity follows. However, in a large majority of cases, the uncertainty can at least be bounded. A range with very wide bounds can often be obtained by considering constraints of physical nature on the quantities of interest. For example, physical considerations make it possible to limit the Poisson ratio of a homogeneous isotropic material between –1 and 0.5. Even if relatively narrow, this range is not very informative. The opinion of an expert, on the other hand, could allow this range to be further significantly reduced. In our example, an expert could, for example, state that, for the material that we are considering, the Poisson ratio will be between 0.2 and 0.4. Note that, based on this information, we cannot characterize how the uncertainty varies within this range (are the boundary values as plausible as the center values?). Nonetheless, there are situations where a range is the only information available.
Interval analysis can be used to model such cases where the uncertainty is provided by bounds on the quantity of interest. The uncertainty on the quantities x 1, …, xn is then described by their lower bound  and their upper bound
and their upper bound  . A lot of research work has then focused on the propagation of uncertainties from x 1, …, xn to a quantity y = g ( x 1, …, xn ), where g is any function modeling the relation between the input and output variables. The problem of determining the lower and upper bound on y is equivalent to solving a global optimization problem. Consequently, many global optimization algorithms can be applied to solve this problem (Hansen and Walster 2003). Note that in cases where the function g is monotonic over the range of variation of the input variables (namely, on the range domain), then the lower and upper bounds on y can be determined very efficiently: due to the monotonicity, y has merely to be evaluated at the vertices of the hypercube constituted by the bounds of the input variables. The lower and upper bounds are then necessarily the minimum and maximum among these points, respectively. This method is often known as the vertex method. Other techniques use Taylor expansions to approximate the bounds on the output variable. Note that sampling techniques, such as Monte-Carlo simulation, can also be used to solve this problem, but this quickly becomes prohibitively time-consuming and methods using global optimization algorithms are usually more efficient. For a review of the different algorithms for efficient interval analysis, the reader may refer to Kreinovich and Xiang (2008).
. A lot of research work has then focused on the propagation of uncertainties from x 1, …, xn to a quantity y = g ( x 1, …, xn ), where g is any function modeling the relation between the input and output variables. The problem of determining the lower and upper bound on y is equivalent to solving a global optimization problem. Consequently, many global optimization algorithms can be applied to solve this problem (Hansen and Walster 2003). Note that in cases where the function g is monotonic over the range of variation of the input variables (namely, on the range domain), then the lower and upper bounds on y can be determined very efficiently: due to the monotonicity, y has merely to be evaluated at the vertices of the hypercube constituted by the bounds of the input variables. The lower and upper bounds are then necessarily the minimum and maximum among these points, respectively. This method is often known as the vertex method. Other techniques use Taylor expansions to approximate the bounds on the output variable. Note that sampling techniques, such as Monte-Carlo simulation, can also be used to solve this problem, but this quickly becomes prohibitively time-consuming and methods using global optimization algorithms are usually more efficient. For a review of the different algorithms for efficient interval analysis, the reader may refer to Kreinovich and Xiang (2008).
A major disadvantage of interval approaches is the lack of a measure of uncertainty, similar to probability within the context of probability theory. In interval analysis, uncertainty is characterized by the boundaries of the interval only, but no information is available on the likelihood of different values within that interval. In probabilistic approaches, the likelihood of different values is characterized by the PDF, which defines the probability that the quantity of interest lies within a certain range (for example, an interval). Such a measure is not available in the interval approach.
Interval arithmetic and associated uncertainty propagation methods will not be discussed in more detail because of the lack of an uncertainty measure in interval analysis. This reduces the usefulness of the method for reliability- or robustness-based applications where quantification of the risk associated with various decisions is required. Nevertheless, the interval approach is still useful in situations where only the worst case needs to be considered.
While bounds on an interval may be sufficient to quantify epistemic uncertainty within the context of interval analysis, there are many situations where additional information is available, making it possible to refine uncertainty quantification.
Let us consider the case where experts believe that the Poisson ratio of a material is bounded by the interval [0.2;0.4] for a given material. It is very likely that, with their expertise, they will be able to provide a more refined analysis. For example, they can state that most of the time the Poisson ratio of the material will be between 0.3 and 0.35 and only in rare cases it will fall outside this narrower range. This information on the epistemic uncertainty provided by experts can be modeled within the context of fuzzy set theory by a trapezoidal membership function, as illustrated in Figure 1.6. The values in the interval [0.3;0.35] are the most likely values and their corresponding value in terms of the membership function is 1. The membership function then linearly decreases down to the bounds 0.2 and 0.4 provided by the experts. For any value α of the membership function, we can obtain an interval on the quantity of interest, called α -cut. In the example in Figure 1.6, we illustrate the interval for a level α = 0.6, denoted 0.6-cut.
Triangular membership functions are also frequently used in fuzzy set theory. They allow a single value to be modeled as the most probable, as well as bounds outside which the quantity of interest cannot be located. More generally, any kind of membership functions can be used, but this is very rare, in practice, because of the difficulty of specifying them for concrete problems.
Читать дальше

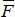 and F in practice, especially in the presence of small amounts of data (a small number of samples or even no samples at all and only the availability of expert opinions, etc.). Indeed, when few samples are available, the bounding that can usually be obtained on the distribution function is too large to be useful in practice. Sometimes there is even a total absence of samples (that is, there have been no formalized experiments that can be traced and exploited) and only expert opinions can provide information on existing uncertainties. How can the bounds
and F in practice, especially in the presence of small amounts of data (a small number of samples or even no samples at all and only the availability of expert opinions, etc.). Indeed, when few samples are available, the bounding that can usually be obtained on the distribution function is too large to be useful in practice. Sometimes there is even a total absence of samples (that is, there have been no formalized experiments that can be traced and exploited) and only expert opinions can provide information on existing uncertainties. How can the bounds  and their upper bound
and their upper bound  . A lot of research work has then focused on the propagation of uncertainties from x 1, …, xn to a quantity y = g ( x 1, …, xn ), where g is any function modeling the relation between the input and output variables. The problem of determining the lower and upper bound on y is equivalent to solving a global optimization problem. Consequently, many global optimization algorithms can be applied to solve this problem (Hansen and Walster 2003). Note that in cases where the function g is monotonic over the range of variation of the input variables (namely, on the range domain), then the lower and upper bounds on y can be determined very efficiently: due to the monotonicity, y has merely to be evaluated at the vertices of the hypercube constituted by the bounds of the input variables. The lower and upper bounds are then necessarily the minimum and maximum among these points, respectively. This method is often known as the vertex method. Other techniques use Taylor expansions to approximate the bounds on the output variable. Note that sampling techniques, such as Monte-Carlo simulation, can also be used to solve this problem, but this quickly becomes prohibitively time-consuming and methods using global optimization algorithms are usually more efficient. For a review of the different algorithms for efficient interval analysis, the reader may refer to Kreinovich and Xiang (2008).
. A lot of research work has then focused on the propagation of uncertainties from x 1, …, xn to a quantity y = g ( x 1, …, xn ), where g is any function modeling the relation between the input and output variables. The problem of determining the lower and upper bound on y is equivalent to solving a global optimization problem. Consequently, many global optimization algorithms can be applied to solve this problem (Hansen and Walster 2003). Note that in cases where the function g is monotonic over the range of variation of the input variables (namely, on the range domain), then the lower and upper bounds on y can be determined very efficiently: due to the monotonicity, y has merely to be evaluated at the vertices of the hypercube constituted by the bounds of the input variables. The lower and upper bounds are then necessarily the minimum and maximum among these points, respectively. This method is often known as the vertex method. Other techniques use Taylor expansions to approximate the bounds on the output variable. Note that sampling techniques, such as Monte-Carlo simulation, can also be used to solve this problem, but this quickly becomes prohibitively time-consuming and methods using global optimization algorithms are usually more efficient. For a review of the different algorithms for efficient interval analysis, the reader may refer to Kreinovich and Xiang (2008).










