2.28.1 Null Hypothesis Significance Testing (NHST): A Legacy of Criticism
Criticisms targeted against null hypothesis significance testing have inundated the literature since at least the time Berkson in 1938 brought to light how statistical significance can be easily achieved by simple manipulations of sample size:
I believe that an observant statistician who has had any considerable experience with applying the chi‐square test repeatedly will agree with my statement that, as a matter of observation, when the numbers in the data are quite large, the P' s tend to come out small. (p. 526)
Since Berkson, the very best and renown of methodologists have remarked that the significance test is subject to gross misunderstanding and misinterpretation (e.g., see Bakan, 1966; Carver, 1993; Cohen, 1990; Estes, 1997; Loftus, 1991; Meehl, 1978; Oakes, 1986; Shrout, 1997; Wilson, Miller, and Lower, 1967). And though it can be difficult to assess or evaluate whether the situation has improved, there is evidence to suggest that it has not. Few describe the problem better than Gigerenzer in his article Mindless statistics(Gigerenzer, 2004), in which he discusses both the roots and truths of hypothesis testing, as well as how its “statistical rituals” and practices have become far more of a sociologicalphenomenon rather than anything related to good science and statistics.
Other researchers have found that misinterpretations and misunderstandings about the significance test are widespread not only among students but also among their instructors (Haller and Krauss, 2002). What determines statistical significance and what is it a function of? This is an extremely important question. An unawareness of the determinants of statistical significance leaves the door open to misunderstanding and misinterpretation of the test, and the danger to potentially draw false conclusions based on its results. Too often and for too many, the finding “ p < 0.05” simply denotes a “good thing” of sorts, without ever being able to pinpoint what is so “good” about it.
Recall the familiar one‐sample z ‐test for a mean discussed earlier:
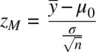
where the purpose of the test was to compare an obtained sample mean 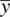 to a population mean μ 0under the null hypothesis that μ = μ 0. Sigma, σ , recall is the standard deviation of the population from which the sample was presumably drawn. Recall that in practice, this value is rarely if ever known for certain, which is why in most cases an estimate of it is obtained in the form of a sample standard deviation s . What determines the size of z M, and therefore, the smallness of p ? There are three inputs that determine the size of p , which we have already featured in our earlier discussion of statistical power. These three factors are
to a population mean μ 0under the null hypothesis that μ = μ 0. Sigma, σ , recall is the standard deviation of the population from which the sample was presumably drawn. Recall that in practice, this value is rarely if ever known for certain, which is why in most cases an estimate of it is obtained in the form of a sample standard deviation s . What determines the size of z M, and therefore, the smallness of p ? There are three inputs that determine the size of p , which we have already featured in our earlier discussion of statistical power. These three factors are 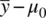 , σ and n . We consider each of these once more, then provide simple arithmetic demonstrations to emphasize how changing any one of these necessarily results in an arithmetical change in z M, and consequently, a change in the observed p ‐value.
, σ and n . We consider each of these once more, then provide simple arithmetic demonstrations to emphasize how changing any one of these necessarily results in an arithmetical change in z M, and consequently, a change in the observed p ‐value.
As a first case, consider the distance 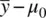 . Given constant values of σ and n , the greater the distance between
. Given constant values of σ and n , the greater the distance between  and μ 0 , the larger z M will be. That is, as the numerator
and μ 0 , the larger z M will be. That is, as the numerator 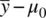 grows larger, the resulting z Malso gets larger in size, which as a consequence, decreases p in size. As a simple example, assume for a given research problem that σ is equal to 20 and n is equal to 100. This means that the standard error is equal to 20/
grows larger, the resulting z Malso gets larger in size, which as a consequence, decreases p in size. As a simple example, assume for a given research problem that σ is equal to 20 and n is equal to 100. This means that the standard error is equal to 20/ 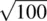 , which is equal to 20/10 = 2. Suppose the obtained sample mean
, which is equal to 20/10 = 2. Suppose the obtained sample mean 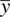 were equal to 20, and the mean under the null hypothesis, μ 0, were equal to 18. The numerator of z Mwould thus be 20 – 18 = 2. When 2 is divided by the standard error of 2, we obtain a value for z Mof 1.0, which is not statistically significant at p < 0.05.
were equal to 20, and the mean under the null hypothesis, μ 0, were equal to 18. The numerator of z Mwould thus be 20 – 18 = 2. When 2 is divided by the standard error of 2, we obtain a value for z Mof 1.0, which is not statistically significant at p < 0.05.
Now, consider the scenario where the standard error of the mean remains the same at 2, but that instead of the sample mean 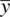 being equal to 20, it is equal to 30. The difference between the sample mean and the population mean is thus 30 – 18 = 12. This difference represents a greater distance between means, and presumably, would be indicative of a more “successful” experiment or study. Dividing 12 by the standard error of 2 yields a z Mvalue of 6.0, which is highly statistically significant at p < 0.05 (whether for a one‐ or two‐tailed test).
being equal to 20, it is equal to 30. The difference between the sample mean and the population mean is thus 30 – 18 = 12. This difference represents a greater distance between means, and presumably, would be indicative of a more “successful” experiment or study. Dividing 12 by the standard error of 2 yields a z Mvalue of 6.0, which is highly statistically significant at p < 0.05 (whether for a one‐ or two‐tailed test).
Having the value of z Mincrease as a result of the distance between 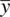 and μ 0increasing is of course what we would expect from a test statistic if that test statistic is to be used in any sense to evaluate the strength of the scientificevidence against the null. That is, if our obtained sample mean
and μ 0increasing is of course what we would expect from a test statistic if that test statistic is to be used in any sense to evaluate the strength of the scientificevidence against the null. That is, if our obtained sample mean 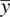 turns out to be very different than the population mean under the null hypothesis, μ 0, we would hope that our test statistic would measure this effect, and allow us to reject the null hypothesis at some preset significance level (in our example, 0.05). If interpreting test statistics were always as easy as this, there would be no misunderstandings about the meaning of statistical significance and the misguided decisions to automatically attribute “worth” to the statement “ p < 0.05.” However, as we discuss in the following cases, there are other ways to make z Mbig or small that do not depend so intimately on the distance between
turns out to be very different than the population mean under the null hypothesis, μ 0, we would hope that our test statistic would measure this effect, and allow us to reject the null hypothesis at some preset significance level (in our example, 0.05). If interpreting test statistics were always as easy as this, there would be no misunderstandings about the meaning of statistical significance and the misguided decisions to automatically attribute “worth” to the statement “ p < 0.05.” However, as we discuss in the following cases, there are other ways to make z Mbig or small that do not depend so intimately on the distance between 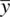 and μ 0, and this is where interpretations of the significance test usually run awry.
and μ 0, and this is where interpretations of the significance test usually run awry.
Consider the case now for which the distance between means,  is, as before, equal to 2.0 (i.e., 20 – 18 = 2.0). As noted, with a standard error also equal to 2.0, our computed value of z Mcame out to be 1.0, which was not statistically significant. However, is it possible to increase the size of z Mwithout changing the observed distance between means? Absolutely. Consider what happens to the size of z Mas we change the magnitude of either σ or n , or both. First, we consider how z Mis defined in part as a function of σ . For convenience, we assume a sample size still of n = 100. Consider now three hypothetical values for σ : 2, 10, and 20. Performing the relevant computations, observe what happens to the size of z Min the case where σ = 2:
is, as before, equal to 2.0 (i.e., 20 – 18 = 2.0). As noted, with a standard error also equal to 2.0, our computed value of z Mcame out to be 1.0, which was not statistically significant. However, is it possible to increase the size of z Mwithout changing the observed distance between means? Absolutely. Consider what happens to the size of z Mas we change the magnitude of either σ or n , or both. First, we consider how z Mis defined in part as a function of σ . For convenience, we assume a sample size still of n = 100. Consider now three hypothetical values for σ : 2, 10, and 20. Performing the relevant computations, observe what happens to the size of z Min the case where σ = 2:
Читать дальше

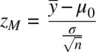
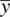 to a population mean μ 0under the null hypothesis that μ = μ 0. Sigma, σ , recall is the standard deviation of the population from which the sample was presumably drawn. Recall that in practice, this value is rarely if ever known for certain, which is why in most cases an estimate of it is obtained in the form of a sample standard deviation s . What determines the size of z M, and therefore, the smallness of p ? There are three inputs that determine the size of p , which we have already featured in our earlier discussion of statistical power. These three factors are
to a population mean μ 0under the null hypothesis that μ = μ 0. Sigma, σ , recall is the standard deviation of the population from which the sample was presumably drawn. Recall that in practice, this value is rarely if ever known for certain, which is why in most cases an estimate of it is obtained in the form of a sample standard deviation s . What determines the size of z M, and therefore, the smallness of p ? There are three inputs that determine the size of p , which we have already featured in our earlier discussion of statistical power. These three factors are 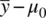 , σ and n . We consider each of these once more, then provide simple arithmetic demonstrations to emphasize how changing any one of these necessarily results in an arithmetical change in z M, and consequently, a change in the observed p ‐value.
, σ and n . We consider each of these once more, then provide simple arithmetic demonstrations to emphasize how changing any one of these necessarily results in an arithmetical change in z M, and consequently, a change in the observed p ‐value.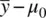 . Given constant values of σ and n , the greater the distance between
. Given constant values of σ and n , the greater the distance between  and μ 0 , the larger z M will be. That is, as the numerator
and μ 0 , the larger z M will be. That is, as the numerator  grows larger, the resulting z Malso gets larger in size, which as a consequence, decreases p in size. As a simple example, assume for a given research problem that σ is equal to 20 and n is equal to 100. This means that the standard error is equal to 20/
grows larger, the resulting z Malso gets larger in size, which as a consequence, decreases p in size. As a simple example, assume for a given research problem that σ is equal to 20 and n is equal to 100. This means that the standard error is equal to 20/ 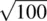 , which is equal to 20/10 = 2. Suppose the obtained sample mean
, which is equal to 20/10 = 2. Suppose the obtained sample mean 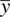 were equal to 20, and the mean under the null hypothesis, μ 0, were equal to 18. The numerator of z Mwould thus be 20 – 18 = 2. When 2 is divided by the standard error of 2, we obtain a value for z Mof 1.0, which is not statistically significant at p < 0.05.
were equal to 20, and the mean under the null hypothesis, μ 0, were equal to 18. The numerator of z Mwould thus be 20 – 18 = 2. When 2 is divided by the standard error of 2, we obtain a value for z Mof 1.0, which is not statistically significant at p < 0.05.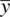 being equal to 20, it is equal to 30. The difference between the sample mean and the population mean is thus 30 – 18 = 12. This difference represents a greater distance between means, and presumably, would be indicative of a more “successful” experiment or study. Dividing 12 by the standard error of 2 yields a z Mvalue of 6.0, which is highly statistically significant at p < 0.05 (whether for a one‐ or two‐tailed test).
being equal to 20, it is equal to 30. The difference between the sample mean and the population mean is thus 30 – 18 = 12. This difference represents a greater distance between means, and presumably, would be indicative of a more “successful” experiment or study. Dividing 12 by the standard error of 2 yields a z Mvalue of 6.0, which is highly statistically significant at p < 0.05 (whether for a one‐ or two‐tailed test).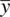 and μ 0increasing is of course what we would expect from a test statistic if that test statistic is to be used in any sense to evaluate the strength of the scientificevidence against the null. That is, if our obtained sample mean
and μ 0increasing is of course what we would expect from a test statistic if that test statistic is to be used in any sense to evaluate the strength of the scientificevidence against the null. That is, if our obtained sample mean 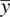 turns out to be very different than the population mean under the null hypothesis, μ 0, we would hope that our test statistic would measure this effect, and allow us to reject the null hypothesis at some preset significance level (in our example, 0.05). If interpreting test statistics were always as easy as this, there would be no misunderstandings about the meaning of statistical significance and the misguided decisions to automatically attribute “worth” to the statement “ p < 0.05.” However, as we discuss in the following cases, there are other ways to make z Mbig or small that do not depend so intimately on the distance between
turns out to be very different than the population mean under the null hypothesis, μ 0, we would hope that our test statistic would measure this effect, and allow us to reject the null hypothesis at some preset significance level (in our example, 0.05). If interpreting test statistics were always as easy as this, there would be no misunderstandings about the meaning of statistical significance and the misguided decisions to automatically attribute “worth” to the statement “ p < 0.05.” However, as we discuss in the following cases, there are other ways to make z Mbig or small that do not depend so intimately on the distance between 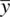 and μ 0, and this is where interpretations of the significance test usually run awry.
and μ 0, and this is where interpretations of the significance test usually run awry. is, as before, equal to 2.0 (i.e., 20 – 18 = 2.0). As noted, with a standard error also equal to 2.0, our computed value of z Mcame out to be 1.0, which was not statistically significant. However, is it possible to increase the size of z Mwithout changing the observed distance between means? Absolutely. Consider what happens to the size of z Mas we change the magnitude of either σ or n , or both. First, we consider how z Mis defined in part as a function of σ . For convenience, we assume a sample size still of n = 100. Consider now three hypothetical values for σ : 2, 10, and 20. Performing the relevant computations, observe what happens to the size of z Min the case where σ = 2:
is, as before, equal to 2.0 (i.e., 20 – 18 = 2.0). As noted, with a standard error also equal to 2.0, our computed value of z Mcame out to be 1.0, which was not statistically significant. However, is it possible to increase the size of z Mwithout changing the observed distance between means? Absolutely. Consider what happens to the size of z Mas we change the magnitude of either σ or n , or both. First, we consider how z Mis defined in part as a function of σ . For convenience, we assume a sample size still of n = 100. Consider now three hypothetical values for σ : 2, 10, and 20. Performing the relevant computations, observe what happens to the size of z Min the case where σ = 2:










