From Lorig et al . (2017), Lemma 3.4, we have
[2.11] 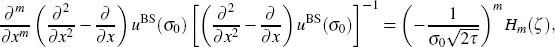
where
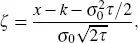
and where
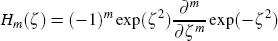
is the m th Hermite polynomial.
We must still calculate the expression in the third line of equation [2.6]for h ≥ 2 (it is equal to 1 when h = 1). From Lorig et al . (2017), Proposition 3.5, we have
[2.12] 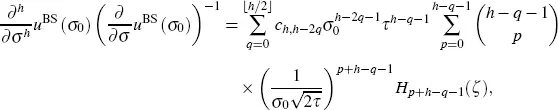
where the coefficients ch,h−2q are defined recursively by
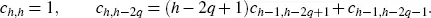
Using equations [2.7]and [2.10], we explicitly calculate:
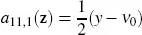
and
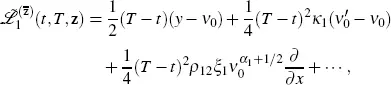
where the dots denote the terms containing 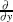 and
and 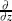 ∙ The functions
∙ The functions 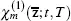 take the form
take the form
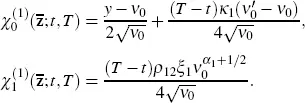
Equation [2.6]gives
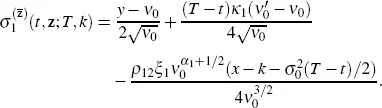
Then,
and
As T → t and k → x, the second and third terms disappear. Calculating the derivative with respect to k , we obtain

and Theorem 2.2 follows.
PROOF OF THEOREM 2.3.-
Equation [2.6]takes the form
[2.13] 
The sets I 2, h are I 2, 1= {(2)}, I 2, 2= {( 1, 1)}. We have a 11, 2(x,y,z) = 0. It follows that equation [2.10]with n = 2 includes only summation over the set I 2, 2and takes the form
While calculating the operator 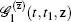 using equation [2.8], we need to calculate only the coefficients of the three partial derivatives with respect to the variable x . We obtain
using equation [2.8], we need to calculate only the coefficients of the three partial derivatives with respect to the variable x . We obtain
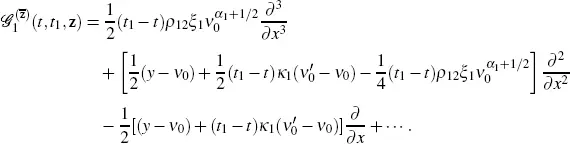
The following integrals are important for calculations:
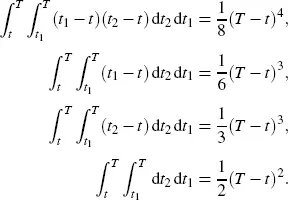
The operator 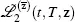 takes the form
takes the form
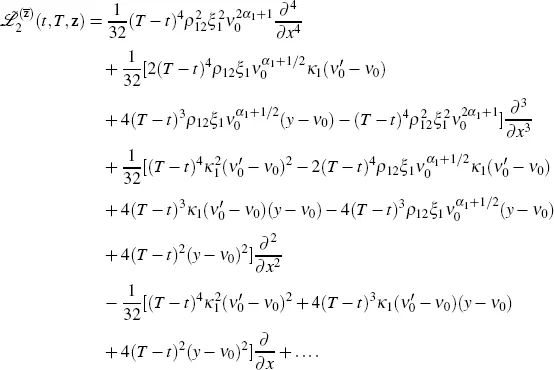
Calculation of the first term on the right-hand side of equation [2.13]using equation [2.11]may be left to the reader.
Next, we calculate the left-hand side of equation [2.12]for h = 2. Using the Hermite polynomials H0(ζ) = 1, H1 (ζ) = 2ζ and H2(ζ) = 4ζ2 - 2, we obtain
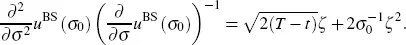
Combining everything together, we obtain the formula for 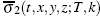
[2.14] 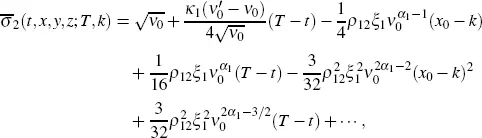
where the ellipsis denotes the terms satisfying the following condition: the limits of the term, its first partial derivative with respect to T and its first two partial derivatives with respect to k as ( T,k ) approaches ( t,x ) within 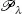 are all equal to 0.
are all equal to 0.
On the right-hand side of equation [2.14], the first term, the partial derivatives with respect to T of the second, fourth and sixth terms, the first partial derivative with respect to k of the third term, and the second partial derivative with respect to k of the fifth term give nonzero contributions to the right-hand side of the asymptotic expansion [2.4].
Gatheral, J. (2008). Consistent modelling of SPX and VIX options. The Fifth World Congress of the Bachelier Finance Society, London.
Latané, H.A. and Rendleman Jr., R.J. (1976). Standard deviations of stock price ratios implied in option prices. J. Finance, 31(2), 369–381.
Lorig, M., Pagliarani, S., Pascucci, A. (2017). Explicit implied volatilities for multifactor local-stochastic volatility models. Math. Finance , 27(3), 926–960.
Orlando, G. and Taglialatela, G. (2017). A review on implied volatility calculation. J. Comput. Appl. Math ., 320, 202–220.
Читать дальше

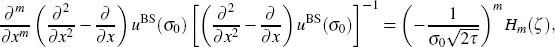
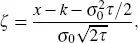
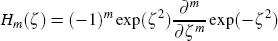
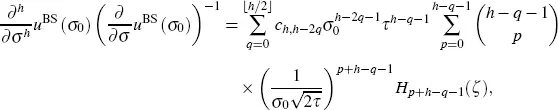
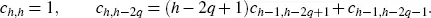
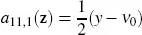
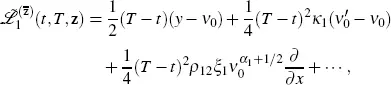
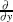 and
and 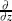 ∙ The functions
∙ The functions 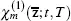 take the form
take the form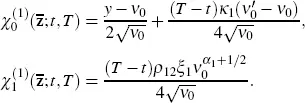
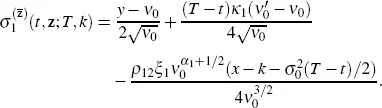
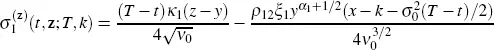
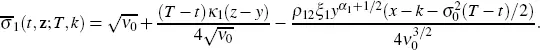

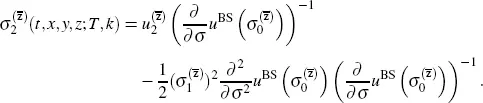
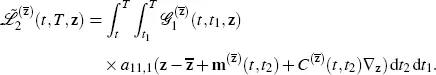
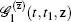 using equation [2.8], we need to calculate only the coefficients of the three partial derivatives with respect to the variable x . We obtain
using equation [2.8], we need to calculate only the coefficients of the three partial derivatives with respect to the variable x . We obtain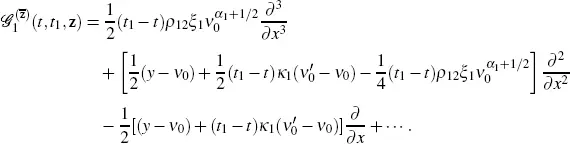
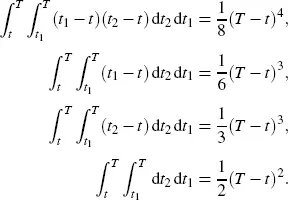
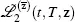 takes the form
takes the form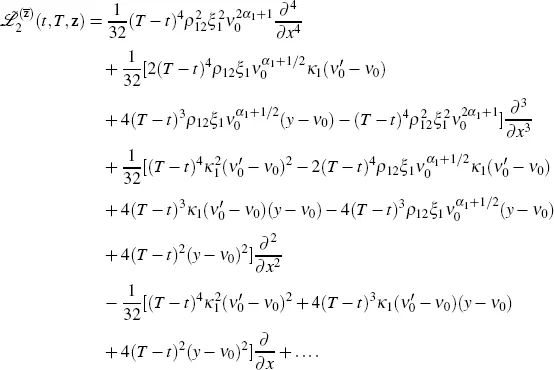
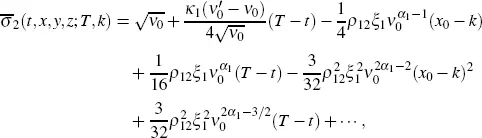
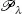 are all equal to 0.
are all equal to 0.










