Applied Modeling Techniques and Data Analysis 2

Agenzia delle Entrate e Ministero dell’Economia e delle Finanze (2018). Convenzione triennale per gli esercizi 2018-2020 [Online]. Available at: https://www.finanze.it/export/sites/finanze/.galleries/Documenti/Varie/DF_CONVENZIONE-MEF_ADE_2018.2020_FIRMATA-28_11_2018.pdf.

Allingham, M.G. and Sandmo, A. (1972). Income tax evasion: A theoretical analysis. Journal of Public Economics , I, 323–338.

Barone, M., Pisani, S., Spingola, A. (2017). Data mining application issues in income indicators audits. Argomenti di discussione – Agenzia delle Entrate , 2.

Basta, S., Fassetti, F., Guarascio, M., Manco, G., Giannotti, F., Pedreschi, D., Spinsanti, L., Papi, G., Pisani, S. (2009). High quality true positive prediction for fiscal fraud detection to regressive conditional. 2009 IEEE International Conference on Data Mining Workshops .

Bonchi, F., Giannotti, F., Mainetto, G., Pedreschi, D. (1999). A classification-based methodology for planning auditing strategies in fraud detection. Proc. of SIGKDD99 , 175–184.

Breiman, L. (1996). Bagging predictors. Machine Learning , 24(2), 123–140.

Corte dei Conti (2016). Il sistema della riscossione dei tributi erariali al 2015. Deliberazione 20 ottobre 2016 , 11/2016/G.

Gonzalez, P.C. and Velasquez, J.D. (2013). Characterization and detection of taxpayers with false invoices using data mining techniques. Expert Systems with Applications , 40(5), 1427–1436.

OpenStax (2013). Introductory Statistics. OpenStax, 19 September [Online]. Available at: http://cnx.org/content/col11562/latest/.

Phua, C., Lee, V., Smith, K., Gayler, R. (2005). A comprehensive survey of data mining-based fraud detection research. Artificial Intelligence Review , submitted.

de Roux, D., Perez, B., Moreno, A., del Pilar Villamil, M., Figueroa, C. (2018). Tax fraud detection for under-reporting declarations using an unsupervised machine learning approach. KDD 2018 , 215–222.

de Sisti, P. and Pisani, S. (2007). Data mining e analisi del rischio di frode fiscale: il caso dei crediti d’imposta. Documenti di lavoro dell’Ufficio Studi – Agenzia delle Entrate , 4.

Wu, R., Ou, C.S., Lin, H., Chang, S., Yen, D. (2012). Using data mining technique to enhance tax evasion detection performance. Expert Systems with Applications , 39, 8769–8777.

1 1 A tax notice is a formal written act through which tax authorities assess a higher due taxable income with respect to the declared one.

2 2 Data analyses are performed using WEKA – the data mining workbench developed at Waikato University in Hamilton, New Zealand, released under the GNU GPL license.

3 3 The IRA sent a total of 59,269 tax notices concerning fiscal year 2012 to self-employed individuals allowed to keep simplified registers, so we can manage a quite significant sample.

Chapter written by Mauro BARONE, Stefano PISANI and Andrea SPINGOLA.

Gatheral’s (2008) double-mean-reverting model by is motivated by empirical dynamics of the variance of stock price. No closed-form solution for European option exists in the above model. In this chapter, we study the behavior of the implied volatility with respect to the logarithmic strike price and maturity near expiry and at-the-money. Using the method by Pagliarani and Pascucci (2017), we explicitly calculate the first few terms of the asymptotic expansion of the implied volatility within a parabolic region.

The history of implied volatility can be traced back at least to Latané and Rendleman (1976), where it appeared under the name “implied standard deviation”, i.e. the standard deviation of asset returns, which are implied in actual European call option prices when investors price options according to the Black-Scholes model. For a recent review of different approaches to determine implied volatility, see Orlando and Taglialatela (2017). To give exact definitions, we use Pagliarani and Pascucci (2017).

In order to briefly explain our contribution to the subject, we will introduce some notations. Let d ≥ 2 be a positive integer, let T0 > 0 be a time horizon, let T ∈ (0 , T 0], and let { Z t: 0 ≤ t ≤ T } be a continuous ℝ d-valued adapted Markov stochastic process on a probability space 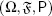with a filtration 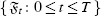. Assume that the first coordinate St of the process Z trepresents the risk-neutral price of a financial asset, and the d - 1 remaining coordinates Y trepresent stochastic factors in a market with zero interest rate and no dividends.

On one hand, we have the time t no-arbitrage price of a European call option with strike price K > 0 and maturity T is Ct,T,K = v ( t , St , Y t , T,K ), where

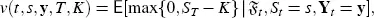
and where ( t, s, y) ∈ [0, T ] × (0 , ∞) × ℝ d 1. We change to logarithmic variables and define the option price by

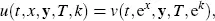
where x is the time t log price of the underlying asset, k is the log strike of the option, and ( t,x, y) ∈ [0 , T ] × ℝ × ℝ d-1.

On the other, the Black-Scholes price in logarithmic variables is

[2.1]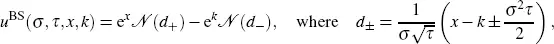

and τ = T − t ∈ [0 , T ], x , k ∈ ℝ, 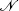is the cumulative distribution function of the standard normal random variable.

DEFINITION 2.1.- The implied volatility σ = σ(t,x, y , T, k) is the unique positive solution of the nonlinear equation

REMARK 2.1.- In the literature on option pricing, there are concepts of model implied volatility and market implied volatility. If the right-hand side of the above equation, i.e. u(t,x,y,T,k), refers to the European option price under a given model, then σ = σ(t,x,y,T,k) is called the model implied volatility. If u(t,x, y ,T,k) is replaced by the observed market option price, then we have the so-called market implied volatility. Here, we work with the (model) implied volatility .