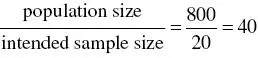Jim Fowler - Practical Statistics for Nursing and Health Care

A common, but misguided, approach to sampling is to first decide what data to collect, then undertake the survey, and finally, decide what analyses should be done. However, without initial thought being given to the aims of the survey, the information or data may not be appropriate (e.g. wrong data collected, or data collected on wrong subjects, or insufficient data collected). As a result, the desired analysis may not be possible or effective.

The key to good sampling is to:

1 Formulate the aims of the study.

2 Decide what analysis is required to satisfy these aims.

3 Decide what data are required to facilitate the analysis.

4 Collect the data required by the survey.

The crucial point relates to the sequence. For example, if the aim of a study is to identify the effectiveness of asthmatic care within a single GP practice, suitable measures of effectiveness need to be defined. One measure could be based on the number of acute asthma exacerbations (deteriorations) in the preceding 12 months, and this number could be compared with that for the previous 12 months. Other measures might assess the number of patients who have had their inhaler technique checked or are using peak flow meters at home. Most of this information can be obtained from practice records, although crosschecking with hospital records may be required to validate the assessment based on acute exacerbations.

We have to distinguish between the target and study populations. The target populationin the asthma example above is the number of patients registered with the GP practice who have asthma. The study populationconsists of all patients who could actually be selected to form the sample, i.e. those who are known to have asthma. For example, a proportion of the target population may not know they have asthma, will not therefore be registered and, thus, will not form part of the study population. Ideally, the ‘target’ and ‘study’ populations coincide.

Once the study population has been defined, the next task is to decide which subjects from the population should form the sample. The following list is not exhaustive, but gives a selection of sample designs:

simple random sampling,

systematic sampling,

stratified sampling,

quota sampling and

cluster sampling.

The first three designs can be applied to sampling from finite populations, i.e. situations where every member of the study population can be identified. Such is the case in our asthmatic care example ( Section 2.4), where a list of all asthmatic patients registered with the GP practice exists. Quota and cluster sampling are used when it is not possible or practicable to enumerate every member of the study population.

In a simple random samplingdesign, every individual in the study population has an equal chance of being included in the sample. That is to say, steps are taken to avoid bias in the sampling. In our asthma example above, the population being sampled is all patients registered with the GP practice who are known to have asthma (say, 800). To select a simple random sample of size n = 20, each patient (‘sampling unit’) is assigned a unique number: 1, 2, 3, and so on, until all 800 patients have been numbered. Then 20 numbers in the range 1–800 are selected at random, and the patients (sampling units) corresponding to these numbers represent the sample.

First, use may be made of random number tables. Appendix A is such a table. The numbers are arranged in groups of five in rows and columns, but this arrangement is arbitrary. Starting at the top left corner, you may read: 2, 3, 1, 5, 7, 5, 4 …; or 23, 15, 75, 48, …; or 231, 575, 485 …; or 23.1, 57.5, 48.5, 90.1, …; and so on, according to your needs. When you have obtained the numbers you need for your investigation, mark the place in pencil. Next time, carry on where you left off. It is possible that a random number will prescribe a subject (sampling unit) that has already been drawn. In this event, ignore the number and take the next random number. The purpose is to eliminate your prejudice as to which items should be selected for measurement. Unfortunately, observer bias, conscious or unconscious, is notoriously difficult to avoid when gathering data in support of a particular hunch!

Second, many calculators and statistical software have a facility for generating random numbers. For example, within LibreOffice Calc spreadsheet typing ‘=RAND()’ within a cell and pressing generates a random number between 0.0 and 1.0 in the form of a decimal fraction, e.g. 0.2771459. To generate more random decimal fractions use the mouse to drag the lower right corner of the cell containing the results of applying the ‘=RAND()’ function down the required number of rows. Please note that many spreadsheets have an auto‐update function whereby formulae are updated after each calculation. To avoid this copy the column of random numbers you have generated and then go to a new cell, right button click your mouse and select ‘Paste Special’ and tick the ‘Numbers’ box and then ‘OK.’ Once you have fixed the random decimal fractions you may use this to provide a set of integers, 2, 7, 7, 1 by multiplying by 10 and using the first digit only; or 27, 71, 45, … by multiplying by 100; or 277, 145; or 2.7, 7.1; and so on, according to your needs.

Random sampling is the preferred approach to sampling. Although it does not guarantee that a representative sample is taken from the study population (due to sampling error, described in Section 10.1), it gives a better chance than any other method of achieving this.

Systematic samplinghas similarities with simple random sampling, in that the first subject in the sample is chosen at random and then every subsequent tenth or twentieth patient (for example) is chosen to cover the entire range of the population.

What interval is required to select a systematic sample of size 20 from a population of 800?

The required fixed interval is:

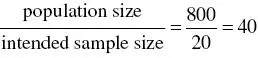
Therefore, the first patient (‘sampling unit’) is selected at random (as described in Section 2.8) from among patients numbered 1–40. Suppose number 23 is selected. The sample then comprises patients 23, 63, 103, 143, …, 783.

A disadvantage of systematic sampling occurs when the patients are listed in the population in some sort of periodic order, and thus we might inadvertently systematically exclude a subgroup of the population. For example, given a population of 800 patients listed by ‘first attendance’ at the clinic, and that over a 20‐week period, 40 patients registered per week, 20 during the daytime and 20 during the evening surgeries. If these patients were listed in the following order: Week 1 daytime patients, Week 1 evening patients, Week 2 daytime patients, …, Week 10 evening patients, then selecting patients 23, 63, …, 783 would result in a sample of evening clinic patients, and exclude all the daytime patients. It is possible that this could generate a biased, or unrepresentative, sample.

An argument in favour of systematic sampling occurs when patients are listed in the population in chronological order, say, by date of first attendance at the GP practice. A systematic sample would yield units whose age distribution is more likely to perfectly represent the study population.