Sergey N. Makarov - Antenna and EM Modeling with MATLAB Antenna Toolbox

(1.10)

In other words, the efficiency is a sole function of the ratio of two resistances. When the loss resistance is zero, the efficiency percentage is 100%; when the loss resistance is equal to the radiation resistance, the efficiency percentage is 50%. The efficiency definition Eq. (1.10)holds for any antenna, whether resonant or not.

For a half‐wave long patch antenna on a lossy dielectric substrate, the ratio of two resistances, R L/ R r, is approximately given by [1]

(1.11)

where h is the patch antenna thickness, W is the patch antenna width, λ 0= c 0/ f is the wavelength in free space at frequency f in Hz, ε ris the relative dielectric constant of the substrate, and tan δ is the loss tangent of the substrate. Determine the antenna efficiency if f = 930 MHz, W = 7 cm, and the substrate is a low‐cost 62 mil FR4 with ε r=4.2 and tan δ =0.02.

Solution:A simple MATLAB script given below programs Eq. (1.11)and outputs R L/ R r= 3.62 and E = 0.22 or 22%. This result is remarkably discouraging; it says that 78% of power supplied to the matched antenna is lost in the antenna substrate itself whereas only 22% of the supplied power is really radiated! Better dielectric substrates with lower loss (and typically of higher cost) must be used at higher frequencies in order to reduce power loss to an acceptable level.

clear all; epsilon = 8.85418782e-012; % Diel. perm. vacuum, F/m mu = 1.25663706e-006; % Magn. perm. vacuum, H/m c = 1/sqrt(epsilon*mu); % Speed of light vacuum, m/s h = 62/1000*2.54e-2; % Patch antenna thickness, m W = 0.07; % Patch antenna width, m eps_r = 4.2; % Rel. diel. constant, FR4 tand = 0.02; % Loss tangent, FR4 f = 930e6; % Frequency, Hz lambda0 = c/f; % Wavelength in vacuum Ratio = 3/32*sqrt(eps_r)*lambda0^2*tand/(h*W) E = 1/(1 + Ratio)

Strictly speaking, practical antennae can be made resonant at only one single frequency, or at a discrete number of them. Unfortunately, no antennas of finite extent exist that are matched at all frequencies.

Consider now a harmonic generator with phasor voltage V g. In frequency domain (in terms of phasors), the generic equivalent TX circuit looks like that shown in Figure 1.3where Z ais the complex antenna impedance , which depends on the antenna frequency. Z ais also called the input impedance to the antenna. The complex impedance is the most important antenna circuit characteristic, the “business card” of the antenna. The generator circuit sees only the antenna impedance; the antenna radiation is not involved. The antenna impedance becomes real at certain frequencies when antenna resonates. Indeed, the equivalent circuit in Figure 1.3is now restricted to harmonic (sinusoidal) RF excitation and is written in terms of phasor voltages and phasor current.

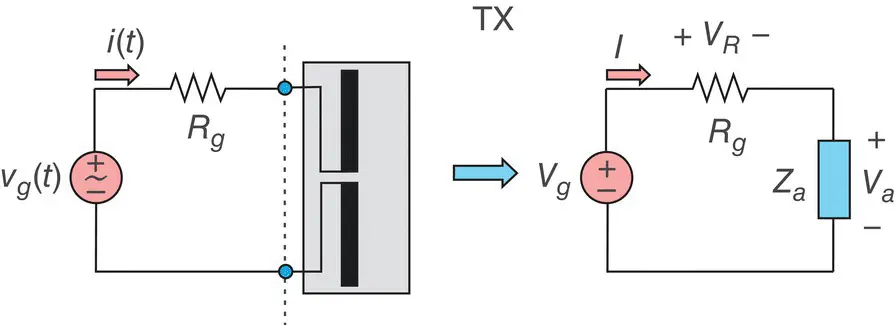
Figure 1.3 A generator (its Thévenin equivalent) connected to an antenna – the equivalent circuit in frequency domain (in the phasor form) for harmonic excitation.

We now write the input antenna impedance for an arbitrary antenna both in rectangular and in the polar form:

(1.12a)

(1.12b)

respectively. The real part of the impedance, R a, is the antenna resistance introduced in the previous text; the imaginary part, X a, is the antenna reactance . The antenna reactance may change its behavior from inductive ( X a> 0) to capacitive ( X a< 0) and vice versa when passing through the resonance.

The angle θ in Eq. (1.12a)and (1.12b)is equivalent to the power angle of a load in power electronics. The problem of antenna impedance matching is essentially equivalent to the problem of power factor correction in power electronics, with the same implications; although different means are used in both those cases. Of primary interest to us is the average power delivered to the antenna. In terms of phasors, this power may be written using several equivalent forms:

(1.13a)

The circuit phasor current in Figure 1.3is given by

(1.13b)

so that the average power delivered to the antenna becomes, according to Eq. (1.13a),

(1.13c)

Similar to Eq. (1.6), it can be shown that its maximum value corresponds to the ideal match , i.e. to X a= 0, R a= R g, that is

(1.13d)

Thus, in order to design an efficient antenna, we must match the antenna impedance to the generator impedance, which has a typical value of 50 Ω. For every antenna type, the matching is usually achieved by changing antenna dimensions and feed geometry.

In order to become familiar with the problem of antenna matching, we now need a practical antenna example and a practical antenna impedance behavior. This example will also help us to define the antenna impedance bandwidth in future. To do so, we consider a cylindrical metal dipole antenna shown in Figure 1.4.

The antenna includes two dipole wings fed by a generator. In Figure 1.4, l Ais the total dipole length, a is the dipole radius.

During the last 70 or so years, a lot of efforts have been made to develop a good analytical terminal dipole model. As a result, one can use the following proven semi‐analytical expression for the input dipole impedance [2]:

(1.14)

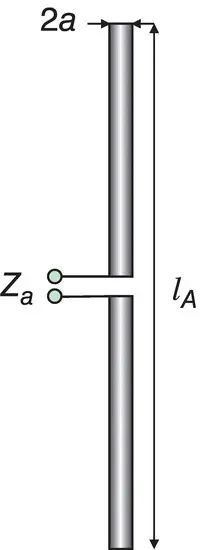
Figure 1.4 Dipole antenna for the evaluation of the reflection coefficient.