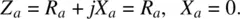The online materials contain a suite of open‐source MATLAB ®scripts along with the supporting supplement, which demonstrate how to implement this approach and how to apply it to antenna reflectors and scatterers of large compared to the wavelength sizes.
We thank Dr. Angelo Puzella of Raytheon Technologies for numerous constructive comments and suggestions.
The Authors
Massachusetts 2021
Some notations used in the text
All complex‐valued Roman quantities are denoted by boldletters. Examples include
1 Vector electric field, time domain
2 Vector electric field, complex phasor in frequency domain
3 Electric field component, time domain
4 Electric field component, complex phasor in frequency domain
All complex‐valued Greek quantities are denoted by the same letters. Examples include
1 Electric potential, time domain
2 Electric potential, complex phasor in frequency domain
Unit vectors in the directions of respective axes are denoted as 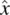 ,
, 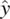 , etc.
, etc.
In spherical co‐ordinates ( 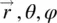 or
or 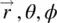 ), θ is always computed from zenith. Azimuthal angle notations φ and ϕ are equivalent; they are used interchangeably.
), θ is always computed from zenith. Azimuthal angle notations φ and ϕ are equivalent; they are used interchangeably.
Time dependency exp( jωt ) is used everywhere.
About the Companion Website
This book is accompanied by a companion website:

www.wiley.com/go/Makarov/AntennaandEMModelingwithMATLAB2e
The companion website is an important part of this text. It provides Antenna Toolbox laboratories in the sequential order. It also provides MATLAB ®codes which employ the Fast Multipole Method (FMM) for large‐size antenna/scattering problems.
CHAPTER 1 Antenna Circuit Model. Antenna Matching. Antenna Bandwidth
SECTION 1 LUMPED CIRCUIT MODEL OF AN ANTENNA. ANTENNA INPUT IMPEDANCE
1.1 Antenna Circuit Model. Antenna Loss
1.2 Maximum Power Transfer to (and from) Antenna
1.3 Antenna Efficiency
1.4 Antenna Input Impedance and Impedance Matching
1.5 Point of Interest: Input Impedance of a Dipole Antenna and Its Dependence on Dipole Length
1.6 Beyond the First Resonance
1.7 Numerical Modeling
References
Problems
1.1 ANTENNA CIRCUIT MODEL. ANTENNA LOSS
The generic transmitter (TX) circuit with an antenna is shown in Figure 1.1. The generator ( g ) is modeled as an ideal (sinusoidal or pulse) voltage source V gin series with the generator resistance R g, connected to a TX antenna. The typical generator resistance is 50 Ω. This model is known as Thévenin equivalent of the generator circuit. The Norton equivalent may also be used when necessary.
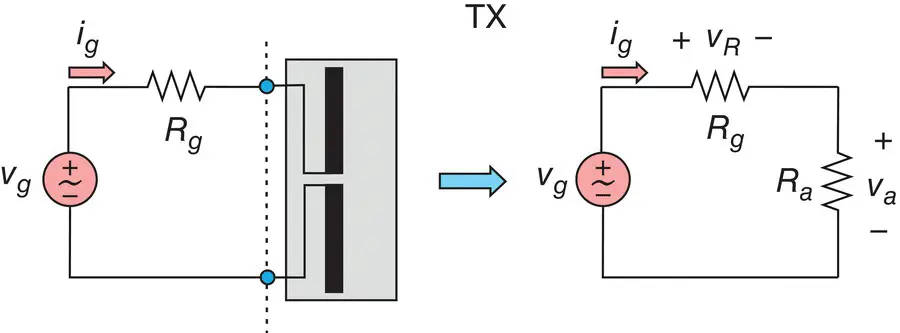
Figure 1.1 A generator (its Thévenin equivalent) connected to an antenna.
The portion depicted in the shaded box is an antenna. The antenna in Figure 1.1is assumed to be resonant , which means that its equivalent impedance, Z a, is purely real, i.e.
(1.1) 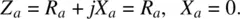
In order words, the resonant antenna is simply modeled by a resistor R a.
The antenna resistance R aincludes two parts:
1 Radiation resistance of the antenna Rr that describes the circuit power loss due to radiation by the antenna into free space.
2 Loss resistance of the antenna RL that describes the circuit power loss in the antenna itself. Case in point: a long thin wire with a significant ohmic resistance or a helical antenna with a ferrite lossy core.
One thus has
(1.2) 
Parasitic antenna resistance R Lhas the following features:
1 it is zero for ideal antennas (a metal antenna made of perfect electric conductors);
2 it is usually relatively small for metal antennas covering the band 0.3–3 GHz (UHF, L‐band, S‐band) where it may be often ignored;
3 it may be very significant for printed antennas on lossy dielectric substrates and in the vicinity of lossy dielectric (such as FR4, ABS, human body, etc.);
4 it is vital for very small antennas whose size is much less than the wavelength.
A small antenna operating at f = 10 MHz uses a thin copper wire with the diameter D of 0.25 mm and with the wire length l of 1 m. Calculate antenna loss resistance R L.
Solution:The DC resistance of the wire is given by
(1.3) 
where σ is the material conductivity and A is the wire cross section. However, we cannot use this formula since most of the high‐frequency current flows in a thin skin layer around the wire. The correct result has the form:
(1.4) 
where P is wire perimeter and μ 0is vacuum permeability. A short MATLAB script given below accomplishes the task and gives R Lapproximately equal to 1 Ω. This value may be comparable to the radiation resistance of a small antenna, and may even exceed it.
clear all; mu = 4*pi*1e-7; % Vacuum permeability, H/m sigma = 5.7e7; % Copper conductivity, S/m D = 0.25e-3; % Diameter, m l = 1; % Length, m f = 10e6; % Frequency, Hz RHF = l/(pi*D)*sqrt(mu*2*pi*f/(2*sigma)) % Loss resistance
1.2 MAXIMUM POWER TRANSFER TO (AND FROM) ANTENNA
One question you have to ask yourself is this: for a fixed resistance R g, can the electric power delivered to the antenna be maximized, and at which value of R adoes the maximum occur? In other words, we would like to know what parameters the antenna should have in order to acquire and radiate maximum electric power from the given RF generator (an RF amplifier). In an electric circuit, the passive load – the antenna – may have only one such parameter – the antenna resistance. All other antenna parameters (geometrical, material, etc.) are implicitly included into antenna's resistance.
Читать дальше

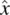 ,
, 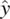 , etc.
, etc.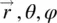 or
or 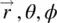 ), θ is always computed from zenith. Azimuthal angle notations φ and ϕ are equivalent; they are used interchangeably.
), θ is always computed from zenith. Azimuthal angle notations φ and ϕ are equivalent; they are used interchangeably.