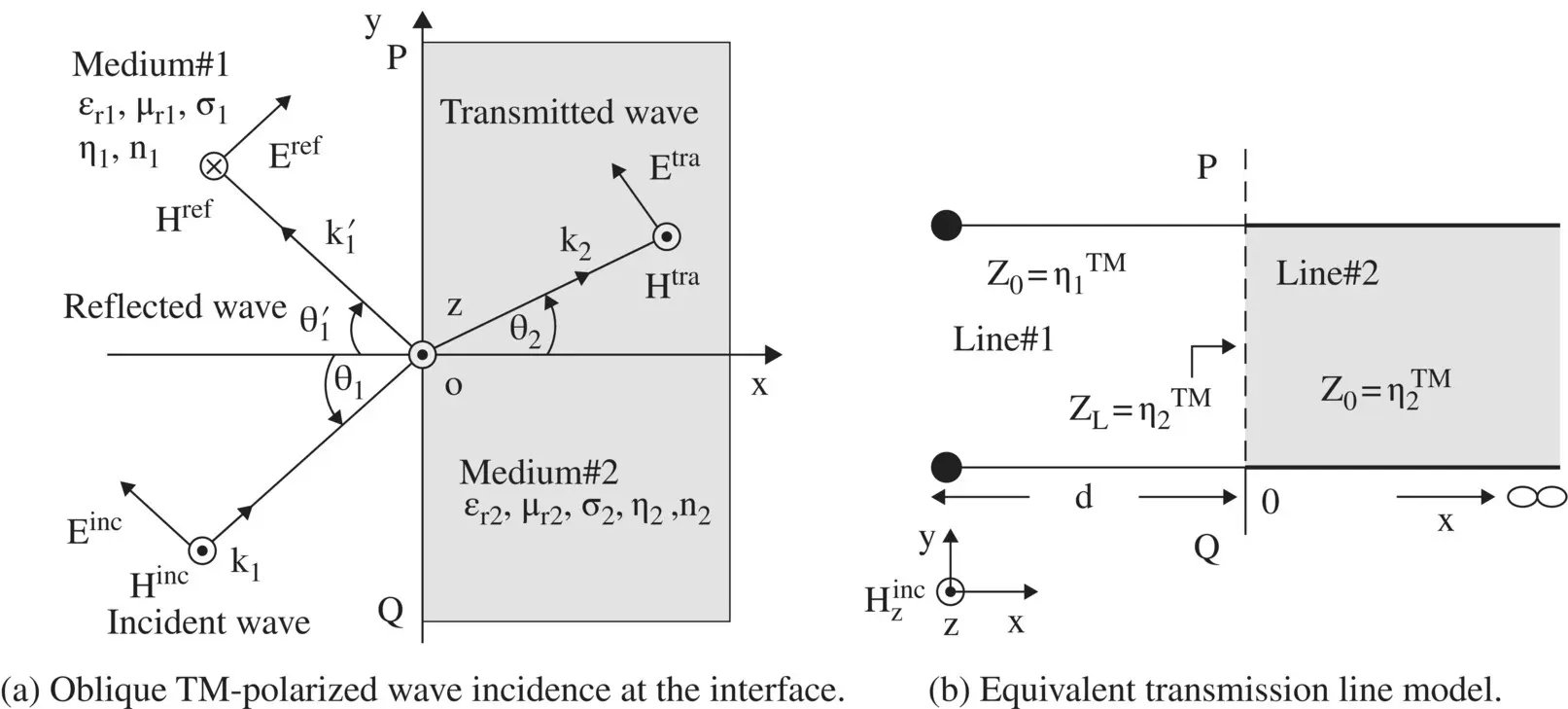
Figure 5.3 Oblique incidence of a plane wave with TM‐polarization at the interface of two media.
(5.2.16) 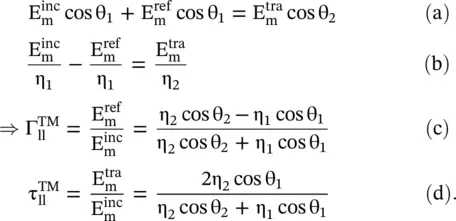
For normal incidence, equations ( 5.2.16c,d) reduce to equations ( 5.1.3a,b). Equations ( 5.2.16c,d) are known as the Fresnel's Equations of the TM‐polarized waves. It is noted that 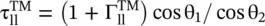 . The total fields in both the media are summarized below:
. The total fields in both the media are summarized below:
Medium #1
The total field is a summation of the incident and reflected fields:
(5.2.17) 
Medium #2
(5.2.18) 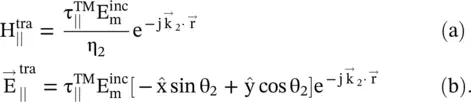
In medium #1, there is a traveling wave along the y ‐axis, whereas, in the direction of normal to the interface, the wave is a standing wave. However, the minima of the standing wave never reach zero levels as 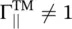 , like a PMC. Again, even if the wave travels in the y‐direction along the interface of two media, the traveling wave is not a surface wave, as in the transverse x‐direction, there is no confinement of field near the interface. However, under certain conditions, discussed in sub section (5.3.2), the surface wave could exist along the interface.
, like a PMC. Again, even if the wave travels in the y‐direction along the interface of two media, the traveling wave is not a surface wave, as in the transverse x‐direction, there is no confinement of field near the interface. However, under certain conditions, discussed in sub section (5.3.2), the surface wave could exist along the interface.
The Oblique Incidence on a Perfect Electric Conductor
If medium #2 is a perfect conductor, 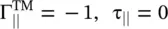 . The medium #1 supports the wave with interference, and the fields are written from equation (5.2.17)as follows:
. The medium #1 supports the wave with interference, and the fields are written from equation (5.2.17)as follows:
(5.2.19) 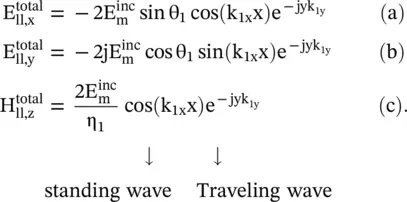
In equation (5.2.19), time‐harmonic dependence e jωtis suppressed. At the surface of the perfect conductor x = 0, the field component 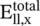 forms the standing wave. However, the standing wave pattern travels along the interface in the y‐direction.
forms the standing wave. However, the standing wave pattern travels along the interface in the y‐direction.
5.2.3 Dispersion Diagrams of Refracted Waves in Isotropic and Uniaxial Anisotropic Media
The dispersion diagrams of the EM-waves in the isotropic and also uniaxial anisotropic medium displaying Snell's law, given in equation (5.2.7), are represented on the (k z− k y)‐plane. Snell's law was obtained from the phase matching of the incident and refracted waves across the boundary of two media. The dispersion diagrams in the isotropic and uniaxial anisotropic media are obtained by continuing the process discussed in subsections ( 4.7.4) and ( 4.7.5) of chapter 4.
Figure (5.4a)shows the geometrical process of constructing the dispersion diagram showing the refraction of the wave at the interface of the air and dielectric media. The incident wavevector 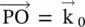 in the air medium (ε r= 1) subtends an angle of incidence θ i. The refracted wavevector
in the air medium (ε r= 1) subtends an angle of incidence θ i. The refracted wavevector 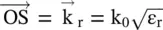 , in the isotropic dielectric medium with relative permittivity ε r, subtends an angle of refraction θ rwith respect to the k z, normal to the interface. Only half of the dispersion circle of each medium is shown. The normal RS intersects the dispersion circle of the isotopic dielectric medium at S. At the interface, the line segments
, in the isotropic dielectric medium with relative permittivity ε r, subtends an angle of refraction θ rwith respect to the k z, normal to the interface. Only half of the dispersion circle of each medium is shown. The normal RS intersects the dispersion circle of the isotopic dielectric medium at S. At the interface, the line segments 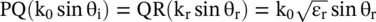 show the phase‐matching across the interface. It is seen that the directions of the phase velocity v pand group velocity v gof the refracted wave are the same.
show the phase‐matching across the interface. It is seen that the directions of the phase velocity v pand group velocity v gof the refracted wave are the same.
Likewise, Fig (5.4b)shows the geometrical construction of double refraction in the uniaxial anisotropic medium. In this case, the line segments PQ(k 0sin θ i) = QR(k rosin θ o= k resin θ e) provide the phase‐matching across the interface. The wavenumbers k roand k rebelong to the refracted ordinary and extraordinary waves . The normal drawn from the location R on the dispersion circle to the interface of air-dielectric medium intersects the dispersion circle of the uniaxial anisotropic medium at S 1for the ordinary waves. It also intersects at the dispersion ellipse at S 2for the extraordinary waves. The wavevectors OS 1and OS 2for the ordinary and extraordinary waves subtend the angle of refraction θ oand θ erespectively with k z‐axis. The first refraction is for the ordinary waves with phase velocity v poand group velocity v goin the same direction. The second refraction, for the extraordinary waves, has phase velocity v peand group velocity v gein different directions. The angles of refraction are different in both cases. The phase and group velocities for both kinds of waves are identical only along the optic axis OO', where the dispersion circle and dispersion ellipse touch each other.
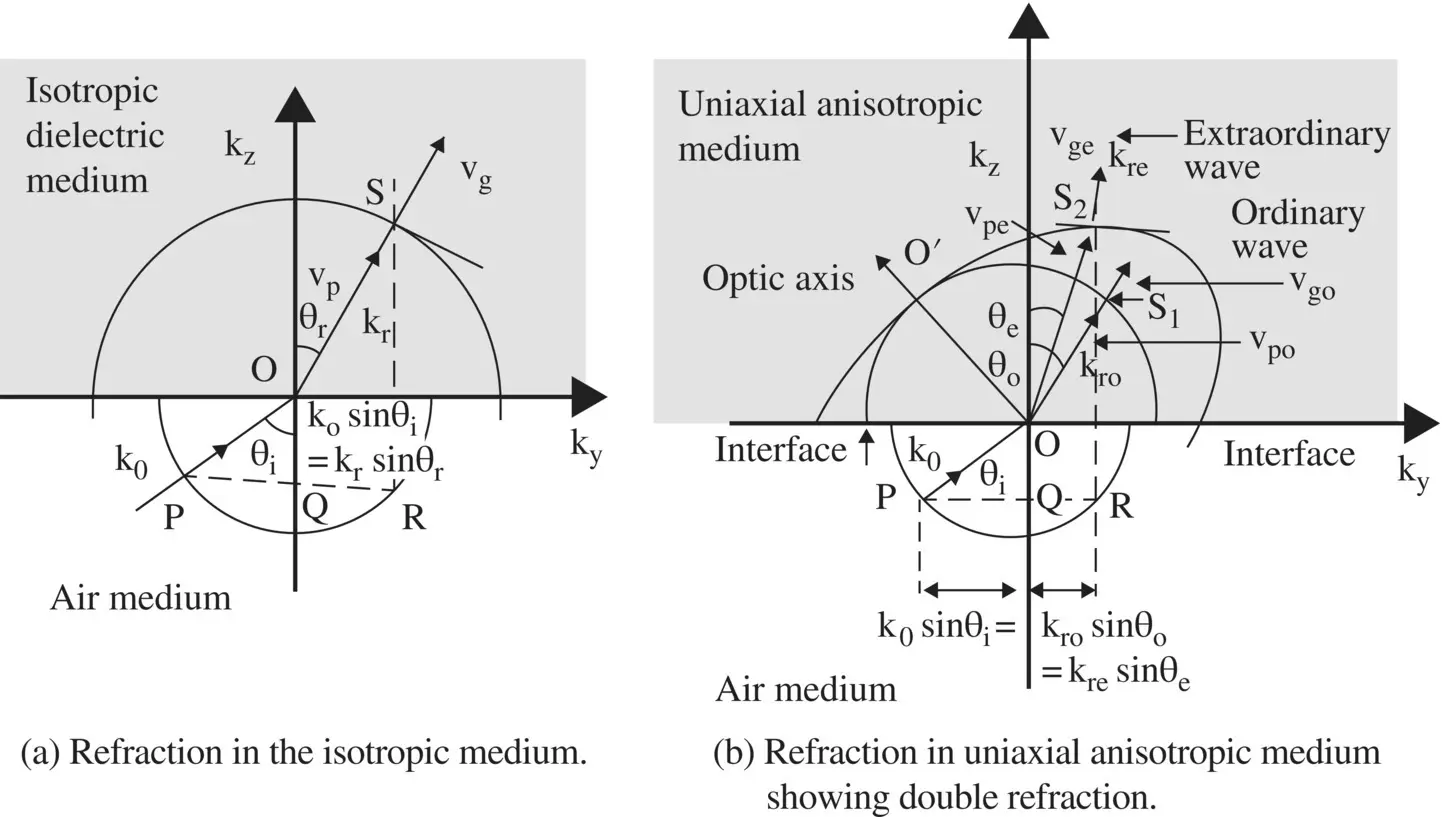
Figure 5.4 Dispersion diagrams of refracted waves.
5.2.4 Wave Impedance and Equivalent Transmission Line Model
The obliquely incident plane wave is partly reflected and partly transmitted at the interface of two electrically dissimilar media. It helps to think the medium #1 and medium #2 as two dissimilar transmission lines with a junction PQ, corresponding to the interface PQ as shown in Figs ( 5.2a)and ( 5.3a)for the TE and TM polarization, respectively. Figures (5.2b)and ( 5.3b)show the equivalent transmission line networks of the composite media, supporting the oblique incidence of the TE and TM‐polarized plane waves. The source connected to the line #1, with characteristic impedance Z 0, corresponding to the wave impedance of the incident wave in medium #1, is assumed to be located at the left of the junction. The line #2 is of an infinite extent that offers a load Z L, corresponding to the wave impedance of the transmitted (refracted) wave in medium #2, at the junction. The reflection and transmission coefficients of the incident wave at the physical media interface correspond to the mismatch, causing reflection and transmission, at the junction of two equivalent lines. Our task is to determine the Z 0and Z Lin terms of the wave impedances of medium #1 and medium #2, respectively, for both the TE and TM polarizations. The correlation between the reflection/transmission coefficient of the TE and TM‐polarized waves at the interface of physical media and reflection/transmission coefficient at the junction of equivalent lines is also be considered.
Читать дальше


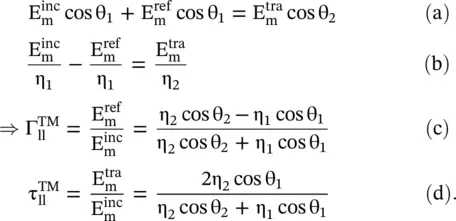
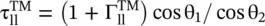 . The total fields in both the media are summarized below:
. The total fields in both the media are summarized below:
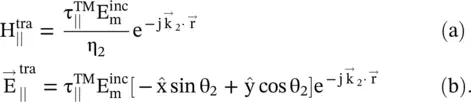
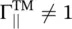 , like a PMC. Again, even if the wave travels in the y‐direction along the interface of two media, the traveling wave is not a surface wave, as in the transverse x‐direction, there is no confinement of field near the interface. However, under certain conditions, discussed in sub section (5.3.2), the surface wave could exist along the interface.
, like a PMC. Again, even if the wave travels in the y‐direction along the interface of two media, the traveling wave is not a surface wave, as in the transverse x‐direction, there is no confinement of field near the interface. However, under certain conditions, discussed in sub section (5.3.2), the surface wave could exist along the interface.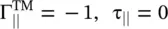 . The medium #1 supports the wave with interference, and the fields are written from equation (5.2.17)as follows:
. The medium #1 supports the wave with interference, and the fields are written from equation (5.2.17)as follows: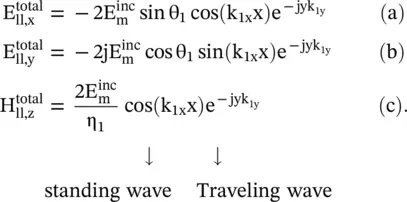
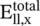 forms the standing wave. However, the standing wave pattern travels along the interface in the y‐direction.
forms the standing wave. However, the standing wave pattern travels along the interface in the y‐direction. in the air medium (ε r= 1) subtends an angle of incidence θ i. The refracted wavevector
in the air medium (ε r= 1) subtends an angle of incidence θ i. The refracted wavevector 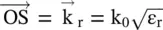 , in the isotropic dielectric medium with relative permittivity ε r, subtends an angle of refraction θ rwith respect to the k z, normal to the interface. Only half of the dispersion circle of each medium is shown. The normal RS intersects the dispersion circle of the isotopic dielectric medium at S. At the interface, the line segments
, in the isotropic dielectric medium with relative permittivity ε r, subtends an angle of refraction θ rwith respect to the k z, normal to the interface. Only half of the dispersion circle of each medium is shown. The normal RS intersects the dispersion circle of the isotopic dielectric medium at S. At the interface, the line segments 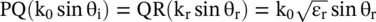 show the phase‐matching across the interface. It is seen that the directions of the phase velocity v pand group velocity v gof the refracted wave are the same.
show the phase‐matching across the interface. It is seen that the directions of the phase velocity v pand group velocity v gof the refracted wave are the same.











