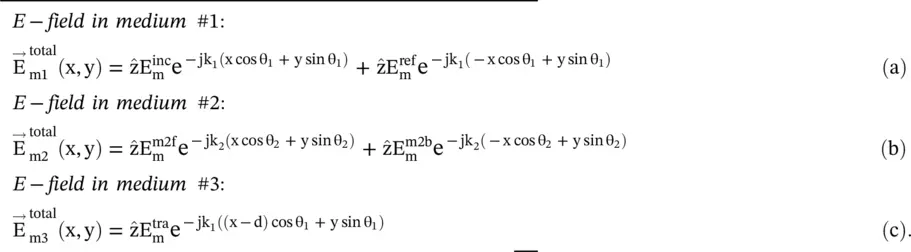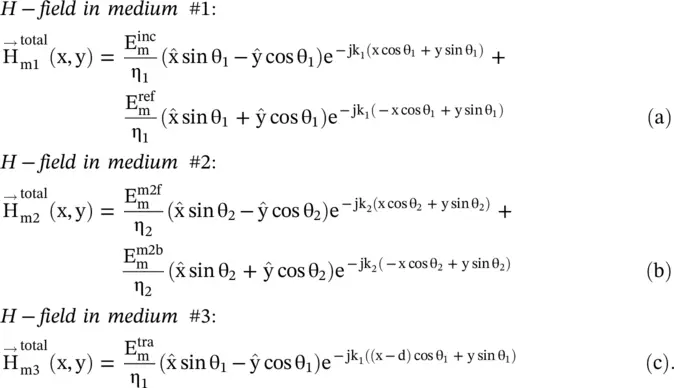(5.3.5) 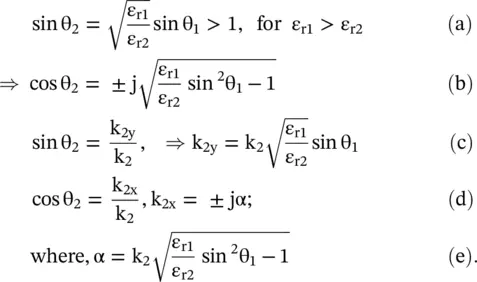
The negative (−) value is selected in further computation as it provides exponentially decaying fields with distance from the interface in the medium #2. The choice of positive (+) value results in the exponentially growing field with the distance that is physically not possible in a usual passive medium. The expressions (5.3.5b,d,e)are used for both the TE and TM polarization to compute the reflection and transmission coefficients, and also the refracted fields in medium #2 for the case θ 1> θ c
Equation (5.2.8c,d)for the reflection and transmission coefficients of the obliquely incident TE‐polarized wave, using an equation (5.3.5a)are reduced to the following expression:
(5.3.6) 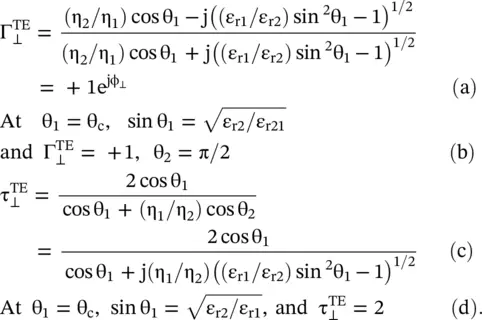
The interface surface acts as a PMC surface for the TE‐polarized incident wave under the case θ 1≥ θ cbecause 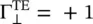 . Over a certain frequency band, it is realized as the artificial magnetic conductor (AMC) surface. At the critical angle, θ 2= π/2, the transmitted wave propagates along the y‐direction at the interface x = 0 +, as shown in Fig (5.5b). For the case θ 1> θ c, shown in Fig (5.5c), the interface supports the slow‐wave type surface wave propagation. It is demonstrated below.
. Over a certain frequency band, it is realized as the artificial magnetic conductor (AMC) surface. At the critical angle, θ 2= π/2, the transmitted wave propagates along the y‐direction at the interface x = 0 +, as shown in Fig (5.5b). For the case θ 1> θ c, shown in Fig (5.5c), the interface supports the slow‐wave type surface wave propagation. It is demonstrated below.
For the case θ 1> θ c, the electric and magnetic field component and power flow of the TE‐polarized wave in the medium #2 is obtained from using equation (5.3.5)with e quation (5.2.10a):
(5.3.7) 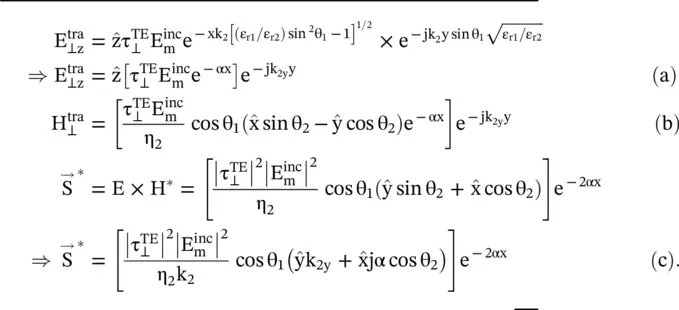
In equation (5.3.7a,b,c), the y‐directed wavevector k 2yand attenuation factor α are given by equation (5.3.5). Equation (5.3.7a,b,c)shows that along the direction normal to the interface, i.e. + x‐direction, the field is exponentially decaying in medium #2; showing the confinement of field near the interface. However, the wave propagates in the y‐direction. It is also evident from the complex Poynting vector giving real power transportation in the y‐direction, while imaginary power shows storages of energy in the x‐directed evanescent field . So the interface supports a surface wave , excited at the interface of two media by the obliquely TE‐polarized incident plane wave at the angle of incidence θ 1≥ θ c. The surface wave, in more detail, is discussed in chapter 7. Its phase velocity along the y‐axis is
(5.3.8) 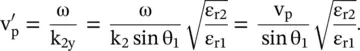
In equation (5.3.8), as ε r1> ε r2; so 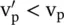 , i.e. the phase velocity of the surface wave is less than that of in the medium #2. Therefore, the surface wave is a slow‐wave.
, i.e. the phase velocity of the surface wave is less than that of in the medium #2. Therefore, the surface wave is a slow‐wave.
All three cases of the angle of incidence apply to the TM‐polarized obliquely incident plane wave. For θ 1> θ c, the reflection and transmission coefficients of the TM‐polarization, given by equation (5.2.28)are reduced to
(5.3.9) 
The electric and magnetic field components of the TM polarization, also the complex Poynting vector in the medium #2 under θ 1> θ c, could be obtained using equation (5.3.5), from equation (5.2.18). The results are summarized below:
(5.3.10) 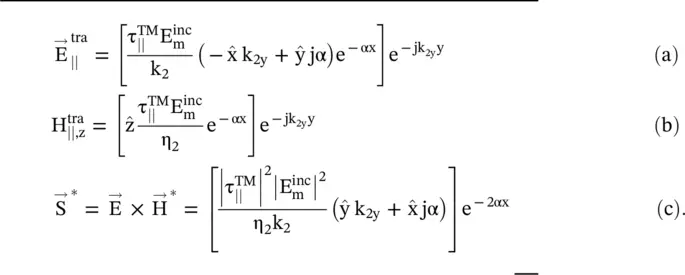
The expression (5.3.9a)shows that there is a total reflection 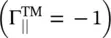 at the interface for θ 1≥ θ c, without any transmission of power from the medium #1 to medium #2. The transmission coefficient shows the presence of the x‐directed evanescent field in the medium #2. Under such conditions, the interface acts as a perfect electrical conductor (PEC); so the interface surface of two media can act as the artificial electric conductor (AEC) . However, there is an exponentially decaying field in the medium #2, and the interface supports the surface wave propagation along the interface at x = 0 +in the y‐direction. The real power carried in the y-direction along the surface is given by the real part of equation (5.3.10). The imaginary part of the Poynting vector shows the stored energy in the evanescent field. Figure (5.5c)shows the surface wave propagation in the y-direction that also occurs in the case of the obliquely incident TE‐polarized waves.
at the interface for θ 1≥ θ c, without any transmission of power from the medium #1 to medium #2. The transmission coefficient shows the presence of the x‐directed evanescent field in the medium #2. Under such conditions, the interface acts as a perfect electrical conductor (PEC); so the interface surface of two media can act as the artificial electric conductor (AEC) . However, there is an exponentially decaying field in the medium #2, and the interface supports the surface wave propagation along the interface at x = 0 +in the y‐direction. The real power carried in the y-direction along the surface is given by the real part of equation (5.3.10). The imaginary part of the Poynting vector shows the stored energy in the evanescent field. Figure (5.5c)shows the surface wave propagation in the y-direction that also occurs in the case of the obliquely incident TE‐polarized waves.
This subsection shows the existence of a surface wave at the interface of natural media. However, artificially engineered metasurfaces discussed in subsection (22.5.5) of chapter 2has additional ability to control the surface wave in the desired manner, and also reradiate it as the leaky wave.
5.4 EM‐Waves Incident at Dielectric Slab
The EM‐waves can strike the slab embedded in a homogeneous medium both normally and obliquely. Both cases of wave incidence and their transmission line models are discussed below. The analysis can be extended to the multilayer medium.
Figure (5.6a)illustrates the oblique incidence of the TE‐polarized waves on a three‐layered dielectric medium. It is desired to find overall reflection and transmission coefficients of a dielectric slab of thickness d embedded in a homogeneous medium, while the TE‐polarized wave is obliquely incident at the first interface located at the y‐axis. The forward and reflected waves are present in both the media #1 and #2 and finally transmitted to the medium #3. The media #1 and #3 have identical electrical properties.
Extending the process given in equations (5.2.1)– (5.2.7), the total E and H‐fields in three media are written as follows:
(5.4.1) 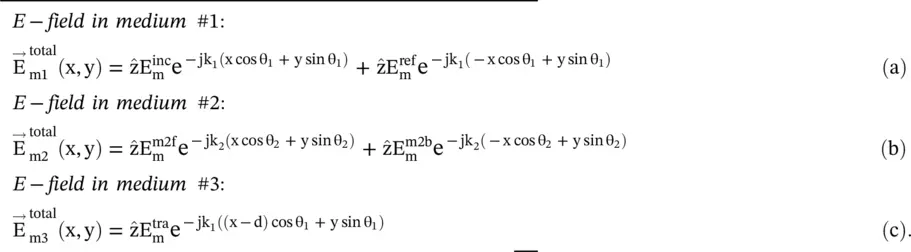
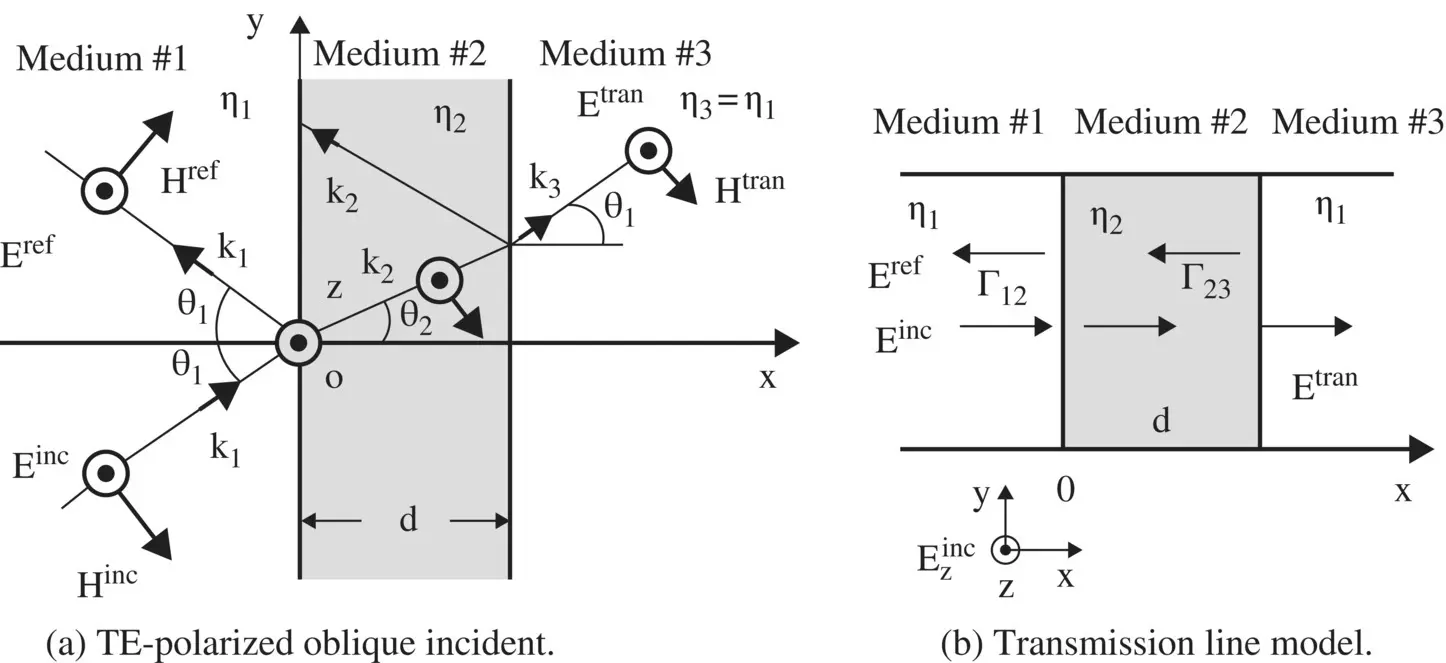
Figure 5.6 Plane‐wave incident on a dielectric slab.
(5.4.2) 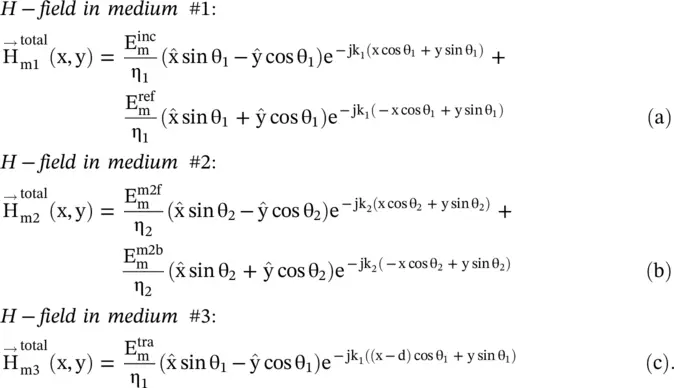
In equations (5.4.2a,b,c)superscripts m 1, m 2, and m 3correspond to medium #1, #2, and #3, respectively. The propagations constant and intrinsic impedance in media are
Читать дальше

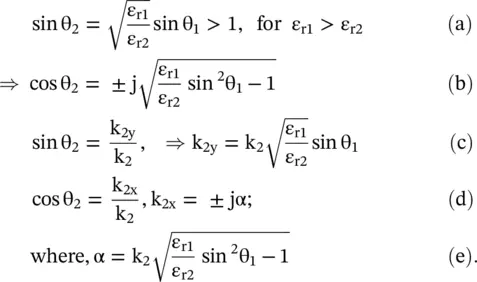
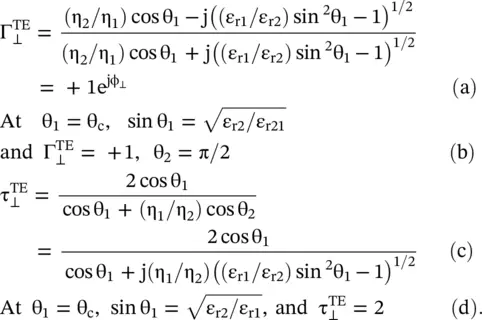
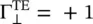 . Over a certain frequency band, it is realized as the artificial magnetic conductor (AMC) surface. At the critical angle, θ 2= π/2, the transmitted wave propagates along the y‐direction at the interface x = 0 +, as shown in Fig (5.5b). For the case θ 1> θ c, shown in Fig (5.5c), the interface supports the slow‐wave type surface wave propagation. It is demonstrated below.
. Over a certain frequency band, it is realized as the artificial magnetic conductor (AMC) surface. At the critical angle, θ 2= π/2, the transmitted wave propagates along the y‐direction at the interface x = 0 +, as shown in Fig (5.5b). For the case θ 1> θ c, shown in Fig (5.5c), the interface supports the slow‐wave type surface wave propagation. It is demonstrated below.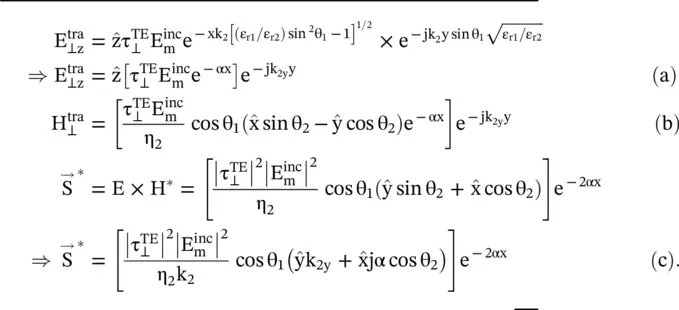
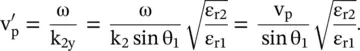
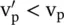 , i.e. the phase velocity of the surface wave is less than that of in the medium #2. Therefore, the surface wave is a slow‐wave.
, i.e. the phase velocity of the surface wave is less than that of in the medium #2. Therefore, the surface wave is a slow‐wave.
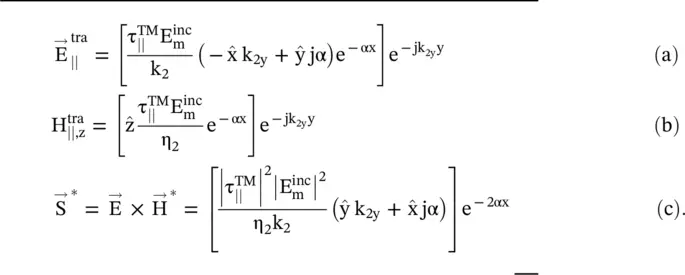
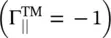 at the interface for θ 1≥ θ c, without any transmission of power from the medium #1 to medium #2. The transmission coefficient shows the presence of the x‐directed evanescent field in the medium #2. Under such conditions, the interface acts as a perfect electrical conductor (PEC); so the interface surface of two media can act as the artificial electric conductor (AEC) . However, there is an exponentially decaying field in the medium #2, and the interface supports the surface wave propagation along the interface at x = 0 +in the y‐direction. The real power carried in the y-direction along the surface is given by the real part of equation (5.3.10). The imaginary part of the Poynting vector shows the stored energy in the evanescent field. Figure (5.5c)shows the surface wave propagation in the y-direction that also occurs in the case of the obliquely incident TE‐polarized waves.
at the interface for θ 1≥ θ c, without any transmission of power from the medium #1 to medium #2. The transmission coefficient shows the presence of the x‐directed evanescent field in the medium #2. Under such conditions, the interface acts as a perfect electrical conductor (PEC); so the interface surface of two media can act as the artificial electric conductor (AEC) . However, there is an exponentially decaying field in the medium #2, and the interface supports the surface wave propagation along the interface at x = 0 +in the y‐direction. The real power carried in the y-direction along the surface is given by the real part of equation (5.3.10). The imaginary part of the Poynting vector shows the stored energy in the evanescent field. Figure (5.5c)shows the surface wave propagation in the y-direction that also occurs in the case of the obliquely incident TE‐polarized waves.